题目内容
17.用适当的方法解方程:①4x2-25=0
②(x2-x)2-5(x2-x)+6=0.
分析 ①先求出x2,再根据平方根的定义进行解答.
②设t=x2-x,把方程t2-5t+6=0的左边分解因式得到(t-2)(t-3)=0,得出方程t-2=0,t-3=0,求出t的值;然后代入来求x的值即可.
解答 解:①整理得,x2=$\frac{25}{4}$,
解得:x1=$\frac{5}{2}$,x2=-$\frac{5}{2}$;
(1)设t=x2-x,则t2-5t+6=0,
整理,得
(t-2)(t-3)=0,
解得t1=2,t2=3,
所以x2-x=2或x2-x=3,
解得x1=2,x2=-1,x3=$\frac{1+\sqrt{13}}{2}$,x3=$\frac{1-\sqrt{13}}{2}$.
点评 本题考查了换元法和直接开平方法解方程.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
7.延长线段AB到点C,使BC=2AB,点D是线段AB的中点,则CD:CB为( )
| A. | 5:2 | B. | 4:5 | C. | 5:4 | D. | 2:1 |
8.-(x-3)去括号后正确的是( )
| A. | x-3 | B. | -x+3 | C. | x+3 | D. | -3-x |
5.下列函数中,y是x的正比例函数是( )
| A. | y=-2x | B. | y=$\frac{2}{x}$ | C. | y=2x2 | D. | y=-2x+1 |
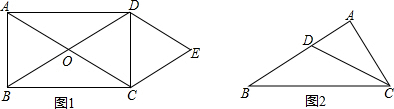
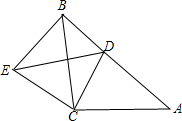 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.