Question

【题目】如图，已知抛物线经过点、，且与轴交于点，抛物线的顶点为，连接，点是线段上的一个动点（不与、）重合.

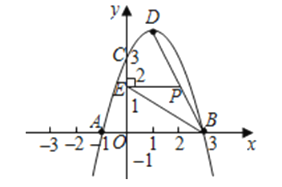
（1）求抛物线的解析式，并写出顶点的坐标；

（2）过点作轴于点，求面积的最大值及取得最大值时点的坐标；

（3）在（2）的条件下，若点是轴上一动点，点是抛物线上一动点，试判断是否存在这样的点，使得以点，，，为顶点的四边形是平行四边若存在，请直接写出点的坐标：若不存在，请说明理由.

Answer 1

【答案】（1），D的坐标为（1，4）；（2）当m=时 △BPE的面积取得最大值为，P的坐标是（，3）；（3）存在，M点的坐标为；；；；；

【解析】

（1）先根据抛物线经过A（-1，0）B（3，0）两点，分别求出a、b的值，再代入抛物线即可求出二次函数的解析式并得出顶点的坐标；

（2）先设出BD解析式y=kx+b，再把B、D两点坐标代入求出k、b的值，得出BD解析式，再根据面积公式即可求出最大值以及点的坐标；

（3）根据题意利用平行四边形的性质进行分析求值，注意分类讨论.

解：（1）∵二次函数y=ax2+bx+3经过点A（﹣1，0）、B（3，0）

∴　　　

所以二次函数的解析式为：

D的坐标为（1，4）

（2）设BD的解析式为y=kx+b

∵过点B（3，0），D（1，4）

∴解得

BD的解析式为span>y = -2x+6

设P（m，）

PE⊥y轴于点E

∴ △BPE的PE边上的高h=

S△BPE=×PE×h

=m()

=

=

∵a=-1<0 当m=时 △BPE的面积取得最大值为

当m=时，y=-2×+6=3

P的坐标是（，3）

（3）存在这样的点，使得以点，，，为顶点的四边形是平行四边形，

当点，，，为顶点的四边形是平行四边形，可得BM平行于PN，则有N点纵坐标等于P点纵坐标，把y=3代入求出N的坐标（0，3）或（2，3），

当N的坐标（0，3）或（2，3）时，根据平行四边形性质求得M点的坐标为　；，；

当BP平行于MN时，根据平行四边形性质求得M点的坐标为；；.

M点的坐标为：　；；；；.