题目内容
如图,已知:⊙O的半径是8,从⊙O外一点P,引圆的两条切线PA,PB,切点分别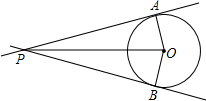 为A,B.
为A,B.(1)若∠APB=70°,求AP的长度(结果精确到0.1);
(2)当OP为何值时,∠APB=90°.
(参考数据:sin35°≈0.5736,cos35°≈0.8191,tan35°≈0.7002,cot35°≈1.4281)
分析:(1)根据切线长定理得到∠APO=35°,再根据锐角三角函数的概念求解;
(2)若∠APB=90°,根据切线长定理发现等腰直角三角形AOP.再根据等腰直角三角形的性质得到OP=
OA.
(2)若∠APB=90°,根据切线长定理发现等腰直角三角形AOP.再根据等腰直角三角形的性质得到OP=
| 2 |
解答:解:(1)∵PA,PB分别切圆于A,B,
∴∠APO=
∠APB=35°.
∴AP=
≈11.4.
(2)若∠APB=90°,根据切线长定理得∠APO=45°.
∴OP=
OA=8
.
∴∠APO=
| 1 |
| 2 |
∴AP=
| OA |
| tan35° |
(2)若∠APB=90°,根据切线长定理得∠APO=45°.
∴OP=
| 2 |
| 2 |
点评:此题主要是运用了切线长定理和锐角三角函数的概念进行求解.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 =
= y=
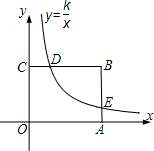
y= ,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.
,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.
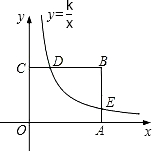
 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=
如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=