题目内容
15. 如图,在△ABC中,分别以AB,AC为边在△ABC外作等边三角形△ABE和△ACD.已知∠ABC=30°,AB=3,BC=4.则BD的长为5.
如图,在△ABC中,分别以AB,AC为边在△ABC外作等边三角形△ABE和△ACD.已知∠ABC=30°,AB=3,BC=4.则BD的长为5.
分析 根据等边三角形的性质得到AE=AB,AD=AC,∠EAB=∠DAC=60°,则∠BAD=∠EAC,再根据三角形全等的判定方法可证得△ACE≌△ADB,根据全等的性质得出BD=CE,再证出∠CBE=90°,由勾股定理求出CE,即可得到结果.
解答 证明:∵△ABE和△ACD是等边三角形,
∴BE=AE=AB=3,AD=AC,∠ABE=∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠CAB,
∴∠BAD=∠EAC,
在△ACE和△ADB中,$\left\{\begin{array}{l}{AE=AB}&{\;}\\{∠EAC=∠DAB}&{\;}\\{AC=AD}&{\;}\end{array}\right.$,
∴△ACE≌△ADB(SAS),
∴BD=CE,
∵∠ABC=30°,
∴∠CBE=∠ABE+∠ABC=90°,
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴BD=5;
故答案为:5.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、勾股定理;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
3. 如图,已知△ABC≌△DEF,且AB=5,BC=6,AC=7,则DF的长为( )
如图,已知△ABC≌△DEF,且AB=5,BC=6,AC=7,则DF的长为( )
 如图,已知△ABC≌△DEF,且AB=5,BC=6,AC=7,则DF的长为( )
如图,已知△ABC≌△DEF,且AB=5,BC=6,AC=7,则DF的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 不能确定 |
7.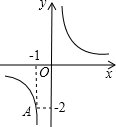 如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
 如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )| A. | k=2 | B. | 图象也经过点B(2,1) | ||
| C. | 若x<-1时,则y<-2 | D. | x>0,y随x的增大而减小 |
 如图,是芝罘区某地各建筑设施的平面位置示意图,每个小正方形的边长为1(单位:千米).
如图,是芝罘区某地各建筑设施的平面位置示意图,每个小正方形的边长为1(单位:千米).
 在平面直角坐标系xOy中,△ABC的位置如图所示.
在平面直角坐标系xOy中,△ABC的位置如图所示.