Question

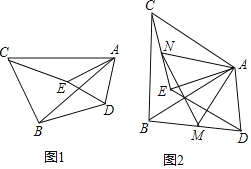
【题目】如图，正方形ABCD的边长为1，AB、AD上各有一点P、Q，△APQ的周长为2，求∠PCQ．

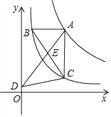
为了解决这个问题，我们在正方形外以BC和AB延长线为边作△CBE，使得△CBE≌△CDQ（如图）

（1）△CBE可以看成由△CDQ怎样运动变化得到的？

（2）图中PQ与PE的长度有什么关系？为什么？

（3）请用（2）的结论证明△PCQ≌△PCE；

（4）根据以上三个问题的启发，求∠PCQ的度数．

（5）对于题目中的点Q，若Q恰好是AD的中点，求BP的长．

Answer 1

【答案】（1）△CBE可以看成是由△CDQ沿逆时针旋转90°得到的；（2）PE=PQ；（3）证明见解析；（4）45°；（5）

【解析】

（1）△CBE可以看成是由△CDQ旋转得到的；

（2）由旋转可知△CEB≌△CDQ，根据全等三角形的对应边相等得到DQ=BE，由正方形的变成为1易知AQ=1-DQ=1-BE，AP=1-BP，又有△APQ的周长为2，可求出PQ=PE；

（3）由（2）得到的PQ=PE，由△CEB≌△CDQ得到一对对应边相等，再由CP为公共边，根据SSS判定△PCQ≌△PCE；

（4）利用△PCQ≌△PCE得出∠PCQ=∠PCE，又有∠BCE=∠QCD，得出∠PCQ的度数是∠DCB度数的一半，由∠DCB为直角即可求出∠PCQ的度数；

（5）由Q为AD的中点，根据正方形的边长为1，求出DQ与AQ的长，又△CEB≌△CDQ，得到BE=DQ，从而求出BE的长，再由△PCQ≌△PCE得到PE=PQ，设PB为x，用PB+BE表示出PE即为PQ的长，且表示出AP的长，在直角三角形APQ中，根据勾股定理列出关于x的方程，求出方程的解得到x的值，即为BP的长．

（1）△CBE可以看成是由△CDQ沿逆时针旋转90°得到的；

（2）∵△CBE≌△CDQ，正方形的边长为1，

∴AQ=1﹣DQ=1﹣BE，AP=1﹣BP，

又∵AP+AQ+PQ=2，

∴1﹣BE+1﹣BP+PQ=2，即2﹣PE+PQ=2，

∴PE=PQ；

（3）∵△CBE≌△CDQ，

∴QC=EC，

在△PCQ和△PCE中，

，

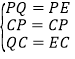∴△PCQ≌△PCE（SSS）；

（4）∵△PCQ≌△PCE，

∴∠PCQ=∠PCE，

又∵∠BCE=∠QCD，

∴∠QCD+∠PCB=∠PCQ，

又∵∠DCB=90°，

∴∠PCQ=×90°=45°；

（5）若Q为AD中点，得到DQ=AQ=AD=，

∵△CBE≌△CDQ，∴BE=DQ=，

设BP=x，则AP=1﹣x，

∵△PCQ≌△PCE，∴QP=PE=PB+BE=x+，

在Rt△APQ中，根据勾股定理得：PQ2=AQ2+AP2，

即（x+）2=（）2+（1﹣x）2，

化简得：x2+x+=+1﹣2x+x2，即3x=1，解得x=，

则BP的长为．