题目内容
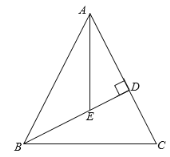
【题目】如图，已知动点A在函数y=
（x＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点P，Q，当QE：DP=9：25时，图中的阴影部分的面积等于___．
【答案】
【解析】
作DF⊥x轴于点F，EG⊥y轴于G，得到△QEG∽△PDF，于是得到
＝
，设EG=9t，则PF=25t，然后根据△ADE∽△FPD，据此即可得到关于t的方程，求得t的值，进而求解．
解：作DF⊥x轴于点F，EG⊥y轴于G，
∴△QEG∽△DPF，
∴＝，
设EG=9t，则PF=25t，
∴A（9t，
），
由AC=AE AD=AB，
∴AE=9t，AD=，DF=，PF=25t，
∵△ADE∽△FPD，
∴AE：DF=AD：PF，
9t：=：25t，即t2=
，
图中阴影部分的面积=
×9t×9t+××=，
故答案为：．
练习册系列答案
阅读快车系列答案
相关题目
