Question

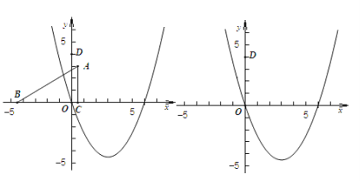
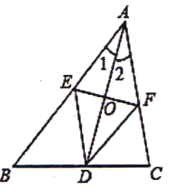
【题目】如图1，点E，F，G分别是等边三角形ABC三边AB，BC，CA上的动点，且始终保持AE=BF=CG，设△EFG的面积为y，AE的长为x，y关于x的函数图象大致为图2所示，则等边三角形ABC的边长为___．

Answer 1

【答案】2

【解析】

设等边三角形ABC边长为a，可得等边三角形ABC的面积为.设AE=x，则BE=a﹣x，可求得S△BEF= ，根据已知条件易证△BEF≌△AGE≌△CFG，即可得y=，根据二次函数的性质可得当x=时，△EFG的面积为最小．根据二次函数的图象可得，，解方程求得a的值即可.

设等边三角形ABC边长为a，则可知等边三角形ABC的面积为.

设AE=x，则BE=a﹣x，

S△BEF= ，

易证△BEF≌△AGE≌△CFG，

y=，

当x= 时，△EFG的面积为最小．

根据二次函数的图象可得，，

解得a=2或a=-2（舍去）.

故答案为：2.