题目内容
17.二元一次方程组$\left\{\begin{array}{l}{x+y=12}\\{2x+y=20}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,则一次函数y=-x+12与y=-2x+20的图象的交点坐标为(8,4).分析 先利用加减消元法解二元一次方程组,然后利用函数图象交点坐标为两函数解析式组成的方程组的解可直接写出一次函数y=-x+12与y=-2x+20的图象的交点坐标.
解答 解:二元一次方程组$\left\{\begin{array}{l}{x+y=12}\\{2x+y=20}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,所以一次函数y=-x+12与y=-2x+20的图象的交点坐标为(8,4).
故答案为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$,(8,4).
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
8.方程x(x+$\frac{1}{2}$)=0的根是( )
| A. | x1=0,x2=$\frac{1}{2}$ | B. | x1=0,x2=-$\frac{1}{2}$ | C. | x1=0,x2=-2 | D. | x1=0,x2=2 |
9.依法纳税是每个公民的义务,《中华人民共和国个人所得税法》规定,有收入的公民依照下表中规定的税率缴纳个人所得税(注:个人所得税的起征点为3500元.即超过3500元的部分需缴纳个人所得税)
2013年第一季度张老师每月收入是相同的,且第一季度个人所得税99元,问张老师每月顶点收入是多少?
| 税级 | 全月应纳所得额 | 税率/% |
| 1 | 不超过1500元的部分 | 3 |
| 2 | 超过1500元至4500元的部分 | 10 |
| 3 | 超过4500元至9000元的部分 | 20 |
| … | … | … |
7.以下函数中,属于一次函数的是( )
| A. | $y=-\frac{x}{2}$ | B. | y=kx+b(k、b为常数) | C. | y=c(c为常数) | D. | $y=\frac{2}{x}$ |
 如图,利用直尺和圆规按下列要求画图.
如图,利用直尺和圆规按下列要求画图.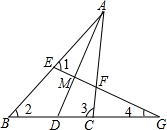 如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).
如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).