题目内容

先化简，再求值：
a+1
2a2-2a
÷
a+1
2a
，其中a=tan60°+
2
sin45°．
考点：分式的化简求值,特殊角的三角函数值
专题：计算题
分析：先求出a的值，再根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．
解答：解：∵a=tan60°+
2
sin45°，
∴a=
3
+
2
×
2
2
=
3
+1，
原式=
a+1
2a(a-1)
÷
a+1
2a

=
a+1
2a(a-1)
×
2a
a+1

=
1
a-1
，
当a=
3
+1时，原式=
1
3
+1-1
=
3
3
．
点评：本题考查的是分式的化简求值及特殊角的三角函数值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象经过顶点（1，4），与y轴相交于点（0，3），将这个二次函数的图象向下平移3个单位，可得到的新函数的解析式为
 
．
比较大小：3.14
 
π；-
2
 
-
3
．
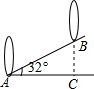如图，坡角为32°的斜坡上两树间的水平距离AC为2米，则两树间的坡面距离AB为（　　）米．
A、2cos32°
B、2tan32°
C、2sin32°
D、
2
cos32°
化简
16
的结果是（　　）
A、2B、-2C、4D、-4
我县2009年平均房价为每平方米2200元．连续两年增长后，2011年平均房价达到每平方米3200元，设这两年平均房价年平均增长率为x，根据题意，可所列方程长为
 
．
甲、乙两人从同一地点出发，沿同一方向跑步，速度分别为4米/秒和6米/秒，开始时甲先跑100米后乙再追赶，则从乙出发开始追上甲这一过程中，甲、乙两人之间的距离s（米）与甲跑步所用时间t（秒）之间的函数关系式为（　　）
A、S=-10t+100（0≤t≤10）
B、S=-2t+100（0≤t≤50）
C、S=-2t+150（25≤t≤75）
D、S=2t-150（0≤t≤75）
求下列各式中的x：
（1）216x3+125=0；
（2）（x+5）3=-27．
如图，在△ABC中，M为BC的中点，MI∥CA，且MI与∠A的平分线AI相交于点I．若AB=10，AC=16，则MI长度为（　　）
A、3
B、
7
2
C、4
D、
9
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网