题目内容
 y=kx-6的图象与横纵轴交于B、A,与y=
y=kx-6的图象与横纵轴交于B、A,与y=| k | x |
分析:首先根据y=kx-6的图象与横纵轴交于B、A可以求得OA=6,OB=
.再根据相似三角形的面积比是相似比的平方,可以求得BD=
,CD=2,从而得到点C的坐标,再根据点C在双曲线上,得到关于k的方程,求得k的值.
| 6 |
| k |
| 2 |
| k |
解答:解:在直线y=kx-6中,
令x=0,则y=-6;
令y=0,则x=
.
即OA=6,OB=
.
又CD∥OA,
∴△AOB∽△COD,
又S△CDB:S△AOB=1:9,
∴BD=
,CD=2,
∴C(
,2).
则有k=
,
又k>0,
则k=4.
令x=0,则y=-6;
令y=0,则x=
| 6 |
| k |
即OA=6,OB=
| 6 |
| k |
又CD∥OA,
∴△AOB∽△COD,
又S△CDB:S△AOB=1:9,
∴BD=
| 2 |
| k |
∴C(
| 8 |
| k |
则有k=
| 16 |
| k |
又k>0,
则k=4.
点评:此题综合运用了相似三角形的判定和性质及反比例函数的图象和性质,要求学生能够根据直线的解析式求得与坐标轴的交点坐标.

练习册系列答案
相关题目
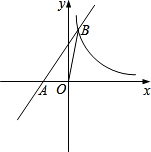 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y= 如图,一次函数y=kx+k的图象与两坐标轴围成的三角形(阴影部分)的面积是
如图,一次函数y=kx+k的图象与两坐标轴围成的三角形(阴影部分)的面积是 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,一次函数y=kx+b的图象与反比例函数
如图,一次函数y=kx+b的图象与反比例函数