题目内容
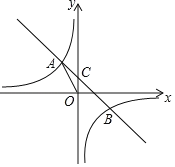
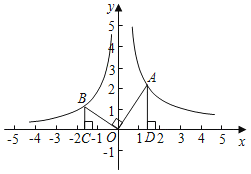
【题目】如图,第一象限内的点A在反比例函数y=![]() 上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=![]() 上,且OA⊥OB,
上,且OA⊥OB,![]() ,BC、AD垂直于x轴于C、D,则k的值为_____.
,BC、AD垂直于x轴于C、D,则k的值为_____.
【答案】﹣![]()
【解析】
利用反比例函数系数的几何意义得到S△AOD=2,接着证明Rt△AOD∽Rt△OBC,利用相似三角形的性质得S△OBC=![]() S△AOD=
S△AOD=![]() ,所以
,所以![]() |k|=
|k|=![]() ,然后根据反比例函数的性质确定k的值.
,然后根据反比例函数的性质确定k的值.
解:如图,∵第一象限内的点A在反比例函数y=![]() 上,BC、AD垂直于x轴于C、D,
上,BC、AD垂直于x轴于C、D,
∴S△AOD=![]() ×4=2,
×4=2,
∵OA⊥OB,
∴∠AOD+∠BOC=90°,
∴∠AOD+∠OAD=90°,
∴∠BOC=∠OAD,
∵∠BCO=∠ODA=90°,
∴Rt△AOD∽Rt△OBC,
∵![]() ,
,
∴
∴S△OBC=![]() S△AOD=
S△AOD=![]() ×2=
×2=![]() ,
,
∴![]() |k|=
|k|=![]() ,
,
而k<0,
∴k=﹣![]() .
.
故答案为﹣![]() .
.


练习册系列答案
相关题目