题目内容
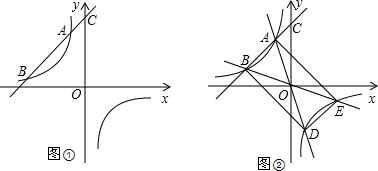
如图①,已知反比例函数y=
(m≠0)的图象经过点A(-1,3),一次函数y=kx+b(k≠0)的图象经过点A和点C(0,4),且与反比例函数的图象相交于另一点B.
(1)求这两个函数的解析式和点B的坐标;
(2)根据图象,直接写出使反比例函数的值大于一次函数的值的x的取值范围;
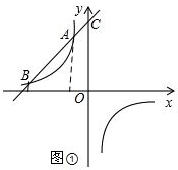
(3)若直线AO、BO分别交双曲线的另一分支于点D、点E,如图②,那么在x轴上是否存在一点G,使得S△AOG=S四边形ABDE?若存在,求出此时G点的坐标;若不存在,说明理由.
| m |
| x |
(1)求这两个函数的解析式和点B的坐标;
(2)根据图象,直接写出使反比例函数的值大于一次函数的值的x的取值范围;
(3)若直线AO、BO分别交双曲线的另一分支于点D、点E,如图②,那么在x轴上是否存在一点G,使得S△AOG=S四边形ABDE?若存在,求出此时G点的坐标;若不存在,说明理由.

考点:反比例函数综合题,待定系数法求一次函数解析式,待定系数法求反比例函数解析式,平行四边形的判定与性质,中心对称图形
专题:综合题
分析:(1)只需运用待定系数法就可求出两个函数的解析式,然后只需将两个函数的解析式组成方程组,解这个方程组就可求出点B的坐标.
(2)利用数形结合就可解决问题.
(3)易证四边形ABDE是平行四边形,就可得到S四边形ABDE=4S△OAB,然后只需运用割补法求出△OAB的面积,就可得到△AOG的面积,就可求出OG的长,就可得到点G的坐标.
(2)利用数形结合就可解决问题.
(3)易证四边形ABDE是平行四边形,就可得到S四边形ABDE=4S△OAB,然后只需运用割补法求出△OAB的面积,就可得到△AOG的面积,就可求出OG的长,就可得到点G的坐标.
解答:解:∵反比例函数y=
(m≠0)的图象经过点A(-1,3),
∴m=-1×3=-3.
∵一次函数y=kx+b(k≠0)的图象经过点A和点C(0,4),
∴
,
解得:
,
∴反比例函数的解析式为y=-
,一次函数的解析式为y=x+4.
解方程组
,
得:
,
,
∴点B的坐标为(-3,1).
(2)∵点A的坐标为(-1,3),点B的坐标为(-3,1),
∴结合图①可得:
当反比例函数的值大于一次函数的值时,x的取值范围为:x<-3或-1<x<0.
(3)过点A作AN⊥x轴于N,点B作BM⊥x轴于M,如图②.
∵直线AO、BO、反比例函数y=-
的图象都是以原点为对称中心的中心对称图形,
∴OA=OD,OB=OE,
∴四边形ABDE是平行四边形,
∴S四边形ABDE=4S△OAB.
∵S△AOG=S四边形ABDE,
∴S△AOG=4S△OAB.
∵点A的坐标为(-1,3),点B的坐标为(-3,1),
∴ON=1,AN=3,OM=3,BM=1,
∴S△OAB=S四边形ABMO-S△BMO
=S梯形ABMN+S△ANO-S△BMO
=
(BM+AN)•MN+
ON•AN-
OM•BM
=
×(1+3)×(3-1)+
×1×3-
×3×1
=4,
∴S△AOG=4S△OAB=16.
∵点G在x轴上,
∴S△AOG=
OG•AN=
×3OG=
OG=16,
∴OG=
,
∴点G的坐标为(
,0)或(-
,0).
| m |
| x |
∴m=-1×3=-3.
∵一次函数y=kx+b(k≠0)的图象经过点A和点C(0,4),
∴
|
解得:
|
∴反比例函数的解析式为y=-
| 3 |
| x |
解方程组
|
得:
|
|
∴点B的坐标为(-3,1).
(2)∵点A的坐标为(-1,3),点B的坐标为(-3,1),
∴结合图①可得:

当反比例函数的值大于一次函数的值时,x的取值范围为:x<-3或-1<x<0.
(3)过点A作AN⊥x轴于N,点B作BM⊥x轴于M,如图②.

∵直线AO、BO、反比例函数y=-
| 3 |
| x |
∴OA=OD,OB=OE,
∴四边形ABDE是平行四边形,
∴S四边形ABDE=4S△OAB.
∵S△AOG=S四边形ABDE,
∴S△AOG=4S△OAB.
∵点A的坐标为(-1,3),点B的坐标为(-3,1),
∴ON=1,AN=3,OM=3,BM=1,
∴S△OAB=S四边形ABMO-S△BMO
=S梯形ABMN+S△ANO-S△BMO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4,
∴S△AOG=4S△OAB=16.
∵点G在x轴上,
∴S△AOG=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴OG=
| 32 |
| 3 |
∴点G的坐标为(
| 32 |
| 3 |
| 32 |
| 3 |
点评:本题主要考查了用待定系数法求一次函数及反比例函数的解析式、中心对称图形的性质、平行四边形的判定与性质、解方程组等知识,运用数形结合是解决第(2)小题的关键,运用割补法是解决第(3)小题的关键.

练习册系列答案
相关题目
 如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为( )
如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为( )A、6
| ||
| B、12cm | ||
C、6
| ||
D、4
|
如果单项式-3x4a-by2与
x3ya+b是同类项,则这两个单项式的和是( )
| 1 |
| 3 |
| A、x6y4 | ||
| B、-x3y2 | ||
C、-
| ||
| D、-x6y4 |
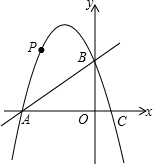 如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.
如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.