题目内容
 在△ABC中EF是BC的垂直平分线,AF、BE交于一点D,AB=AF,求证:AD=DF.
在△ABC中EF是BC的垂直平分线,AF、BE交于一点D,AB=AF,求证:AD=DF.考点:平行四边形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:首先过A作AG∥EF,分别交BE,BC于H,G两点,连结HF,再证明四边形AHFE为平行四边形,进而得出答案.
解答: 证明:过A作AG∥EF,分别交BE,BC于H,G两点,连结HF
证明:过A作AG∥EF,分别交BE,BC于H,G两点,连结HF
∵EF⊥BC,AG∥EC
∴AG⊥BC
∵AB=AF
∴AG是三角形ABF的中垂线
∴BH=FH,
∴∠HBC=∠HFB,
∵EF是BC的垂直平分线,
∴BE=CE,
∴∠ECB=∠HBC,
∴∠ECB=∠HFB,
∴HF∥AC,即AE∥HF,
又∵AH∥EF,
∴四边形AHFE为平行四边形,
∴AD=DF.
 证明:过A作AG∥EF,分别交BE,BC于H,G两点,连结HF
证明:过A作AG∥EF,分别交BE,BC于H,G两点,连结HF∵EF⊥BC,AG∥EC
∴AG⊥BC
∵AB=AF
∴AG是三角形ABF的中垂线
∴BH=FH,
∴∠HBC=∠HFB,
∵EF是BC的垂直平分线,
∴BE=CE,
∴∠ECB=∠HBC,
∴∠ECB=∠HFB,
∴HF∥AC,即AE∥HF,
又∵AH∥EF,
∴四边形AHFE为平行四边形,
∴AD=DF.
点评:此题主要考查了平行四边形的判定与性质以及线段垂直平分线的性质,得出∠ECB=∠HFB是解题关键.

练习册系列答案
相关题目
满足532+m2=522+n2(0<m<n<53)的整数对(m、n)共有( )
| A、3对 | B、4对 | C、6对 | D、8对 |
若点A(7,y1)、B(5,y2)在双曲线y=
上,则y1和y2的关系为( )
| 2 |
| x |
| A、y1<y2 |
| B、y1>y2 |
| C、y1=y2 |
| D、以上答案都不对 |
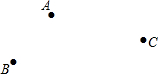 作图题(要求:尺规作图,不写作法,保留作图痕迹)如图,平面上有三个村庄A、B、C,现计划打一水井P,使水井P到三个村庄的距离相等.
作图题(要求:尺规作图,不写作法,保留作图痕迹)如图,平面上有三个村庄A、B、C,现计划打一水井P,使水井P到三个村庄的距离相等. 已知圆锥的底面半径为r=20cm,高h=20
已知圆锥的底面半径为r=20cm,高h=20