题目内容
4.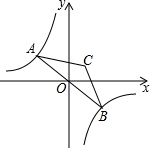 如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )
如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意得出△AOD∽△OCE,进而得出$\frac{AD}{EO}$=$\frac{DO}{EC}$=$\frac{AO}{CO}$,即可得出k=EC×EO=2.
解答 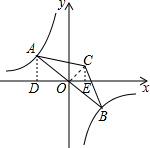 解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,
解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,
∵连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴$\frac{AD}{EO}$=$\frac{DO}{EC}$=$\frac{AO}{CO}$=tan60°=$\sqrt{3}$,则$\frac{{S}_{△ADO}}{{S}_{△COE}}$=3,
∵点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,
∴$\frac{1}{2}$|xy|=$\frac{1}{2}$AD•DO=$\frac{1}{2}$×6=3,
∴$\frac{1}{2}$k=$\frac{1}{2}$EC×EO=1,
则EC×EO=2.
故选:B.
点评 此题主要考查了反比例函数与一次函数的交点以及相似三角形的判定与性质,得出△AOD∽△OCE是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.
如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.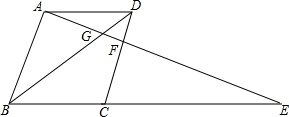 如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.
如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.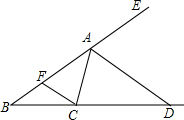 如图,已知在△ABC中,AD是△ABC的外角平分线,交BC的延长线于D,CF∥AD.若AC=3cm,则AF=3cm.
如图,已知在△ABC中,AD是△ABC的外角平分线,交BC的延长线于D,CF∥AD.若AC=3cm,则AF=3cm.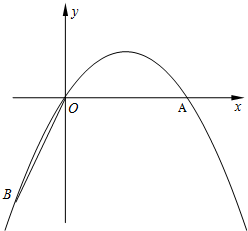 如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.