题目内容
【题目】已知:平行四边形![]() 中,
中,![]() 且
且![]() 平分
平分![]() 交
交![]() 于点
于点![]() , 交
, 交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() ,与线段
,与线段![]() 交于点
交于点![]() ,
,
(1)如果边![]() 长为
长为![]() ,求
,求![]() 的面积.
的面积.
(2)求证:![]()

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求△CBE的面积,只需找到三角形的一边及相应边上的高可求其面积,角平分线和平行线性质易求BE的长,构造BE边上的高,在等腰直角三角形中由勾股定理易求CH的长;
(2)由![]() EG=EN得,.
EG=EN得,.![]() =
=![]() ,可知构建一个等腰直角三角形,作G点关于BE的对称点M,连接ME、MG、MN,证明EMN=90°即可
,可知构建一个等腰直角三角形,作G点关于BE的对称点M,连接ME、MG、MN,证明EMN=90°即可
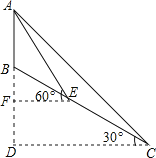
![]() (如图1)过点
(如图1)过点![]() 作
作![]() 的延长线,交于点
的延长线,交于点![]()
![]() 平分
平分![]() ,且
,且![]()
∴∠DCE=∠BCE,∠DCE=∠CEB.
∴![]()
![]()
![]()
∵AD=BD,∠ADB=90°,∴∠A=45°.
∴∠CBM=∠A=45°.
在![]() 中,
中,![]()
![]()
解得![]()
![]()

图1
![]() 证明:(图1的方法)过点
证明:(图1的方法)过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点M
的延长线于点M
![]() 且
且![]()
![]()
又![]() 平分
平分![]() 且
且![]()
∴∠DCE=∠BCE,∠DCE=∠CEB.
∴![]()
∴BE=BC.
又∵AD=BC,AD=BD,
∴![]()

又![]()
![]() 在
在![]() 中
中
![]() 为公共边,
为公共边,![]()
![]()
![]()
又![]()
![]()
又![]()
![]()
由![]()
∵∠GEB+∠GBE=∠MGE=45°,
∴∠GEB=∠GBE.
得![]()
由![]() 是等腰直角三角形得
是等腰直角三角形得![]()
![]()
由![]()
可得![]()
又![]()
![]()
![]()
由![]()
得![]()
![]()
即![]()
![]()

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目