题目内容
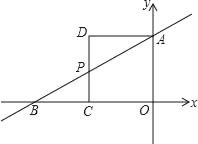
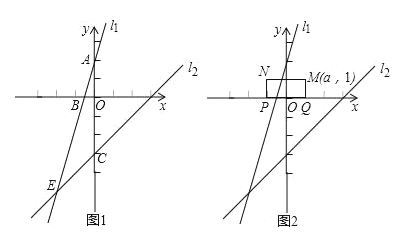
【题目】如图1,在直角坐标系中,一次函数的图象l![]() 与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l
与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l![]() 交于点E(m ,﹣5).
交于点E(m ,﹣5).
(1)m=__________;
(2)直线l![]() 与x轴交于点B,直线l
与x轴交于点B,直线l![]() 与y轴交于点C,求四边形OBEC的面积;
与y轴交于点C,求四边形OBEC的面积;
(3)如图2,已知矩形MNPQ,PQ=2,NP=1,M(a,1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l![]() 或l
或l![]() 有交点,直接写出a的取值范围_____________________________
有交点,直接写出a的取值范围_____________________________
【答案】(1)-2;(2)![]() ;(3)
;(3)![]() ≤a≤
≤a≤![]() 或3≤a≤6.
或3≤a≤6.
【解析】
(1)根据点E在一次函数图象上,可求出m的值;
(2)利用待定系数法即可求出直线l1的函数解析式,得出点B、C的坐标,利用S四边形OBEC=S△OBE+S△OCE即可得解;
(3)分别求出矩形MNPQ在平移过程中,当点Q在l1上、点N在l1上、点Q在l2上、点N在l2上时a的值,即可得解.
解:(1)∵点E(m,5)在一次函数y=x3图象上,
∴m3=5,
∴m=2;
(2)设直线l1的表达式为y=kx+b(k≠0),
∵直线l1过点A(0,2)和E(2,5),
∴![]() ,解得
,解得 ,
,
∴直线l1的表达式为y=![]() x+2,
x+2,
当y=![]() x+2=0时,x=
x+2=0时,x=![]()
∴B点坐标为(![]() ,0),C点坐标为(0,3),
,0),C点坐标为(0,3),
∴S四边形OBEC=S△OBE+S△OCE=![]() ×
×![]() ×5+
×5+![]() ×2×3=
×2×3=![]() ;
;
(3)当矩形MNPQ的顶点Q在l1上时,a的值为![]() ;
;
矩形MNPQ向右平移,当点N在l1上时,![]() x+2=1,解得x=
x+2=1,解得x=![]() ,即点N(
,即点N(![]() ,1),
,1),
∴a![]() +2=
+2=![]() ;
;
矩形MNPQ继续向右平移,当点Q在l2上时,a的值为3,
矩形MNPQ继续向右平移,当点N在l2上时,x3=1,解得x=4,即点N(4,1),
∴a的值为4+2=6,
综上所述,当![]() ≤a≤
≤a≤![]() 或3≤a≤6时,矩形MNPQ与直线l1或l2有交点.
或3≤a≤6时,矩形MNPQ与直线l1或l2有交点.

【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
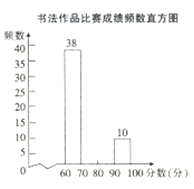
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ______ | 0.32 |
| ______ | ______ |
| 10 | 0.1 |
合计 | ______ | 1 |
根据上述信息,解答下列问题:
(1)请你把表中的数据填写完整.
(2)补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级奖的幅数.