题目内容
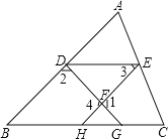
【题目】如图：点D、E、H、G分别在△ABC的边上DE∥BC，∠3=∠B，DG、EH交于点F．求证：∠1+∠2=180°
证明：（请将下面的证明过程补充完整）
∵DE∥BC（已知）
∴∠3=∠EHC（______）
∵∠3=∠B（已知）
∴∠B=∠EHC（______）
∴AB∥EH（______）
∴∠2+∠______=180°（______）
∵∠1=∠4（______）
∴∠1+∠2=180°（等量代换）
【答案】两直线平行内错角相等，等量代换，同位角相等两直线平行，∠4，两直线平行同旁内角互补，对顶角相等
【解析】
利用平行线的判定和性质一一判断即可．
证明：∵DE∥BC(已知)
∴∠3=∠EHC(两直线平行内错角相等)
∵∠3=∠B(已知)
∴∠B=∠EHC(等量代换)
∴AB∥EH(同位角相等两直线平行)
∴∠2+∠4=180°(两直线平行同旁内角互补)
∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)
故答案为：两直线平行内错角相等，等量代换，同位角相等两直线平行，∠4，两直线平行同旁内角互补，对顶角相等．
练习册系列答案
阅读快车系列答案
相关题目
