题目内容
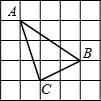 (2012•北海)如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
(2012•北海)如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )分析:由题意可知点A所经过的路径为以C为圆心,CA长为半径,圆心角为60°的弧长,故在直角三角形ACD中,由AD及DC的长,利用勾股定理求出AC的长,然后利用弧长公式即可求出.
解答:解:如图所示:

在Rt△ACD中,AD=3,DC=1,
根据勾股定理得:AC=
=
,
又将△ABC绕点C顺时针旋转60°,
则顶点A所经过的路径长为l=
=
π.
故选C

在Rt△ACD中,AD=3,DC=1,
根据勾股定理得:AC=
| AD2+CD2 |
| 10 |
又将△ABC绕点C顺时针旋转60°,
则顶点A所经过的路径长为l=
60π•
| ||
| 180 |
| ||
| 3 |
故选C
点评:此题考查了弧长公式,以及勾股定理,解本题的关键是根据题意得到点A所经过的路径为以C为圆心,CA长为半径,圆心角为60°的弧长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.
例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.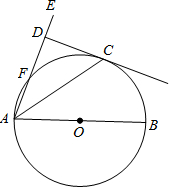 (2012•北海)如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D.
(2012•北海)如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D.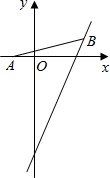 (2012•北海)如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,点B的坐标是
(2012•北海)如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,点B的坐标是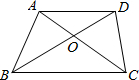 (2012•北海)如图,梯形ABCD中AD∥BC,对角线AC、BD相交于点O,若AO:CO=2:3,AD=4,则BC等于( )
(2012•北海)如图,梯形ABCD中AD∥BC,对角线AC、BD相交于点O,若AO:CO=2:3,AD=4,则BC等于( )