题目内容
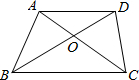（2012•北海）如图，梯形ABCD中AD∥BC，对角线AC、BD相交于点O，若AO：CO=2：3，AD=4，则BC等于（ ）分析：先根据相似三角形的判定定理得出△AOD∽△COB，再由相似三角形的对应边成比例即可得出BC的长．
解答：解：∵梯形ABCD中AD∥BC，
∴∠ADO=∠OBC，∠AOD=∠BOC，
∴△AOD∽△COB，
∵AO：CO=2：3，AD=4，
∴
=
=
，
=
，
解得BC=6．
故选D．
∴∠ADO=∠OBC，∠AOD=∠BOC，
∴△AOD∽△COB，
∵AO：CO=2：3，AD=4，
∴
| AD |
| BC |
| AO |
| CO |
| 2 |
| 3 |
| 4 |
| BC |
| 2 |
| 3 |
解得BC=6．
故选D．
点评：本题考查的是相似三角形的判定与性质，先根据相似三角形的判定定理得出△AOD∽△COB是解答此题的关键．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
例函数图象上的点P，使得四边形PGMC′是平行四边形？如果存在，请求出点M和点P的坐标；如果不存在，请说明理由．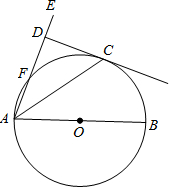
（2012•北海）如图，AB是O的直径，AE交O于点E，且与O的切线CD互相垂直，垂足为D．
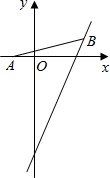（2012•北海）如图，点A的坐标为（-1，0），点B在直线y=2x-4上运动，当线段AB最短时，点B的坐标是
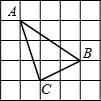（2012•北海）如图，在边长为1的正方形组成的网格中，△ABC的顶点都在格点上，将△ABC绕点C顺时针旋转60°，则顶点A所经过的路径长为（ ）