题目内容
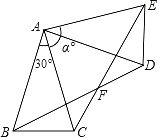
【题目】如图1,直角三角形![]() 的直角顶点
的直角顶点![]() 在矩形
在矩形![]() 的对角线
的对角线![]() 上(点
上(点![]() 不与点
不与点![]() 重合,可与点
重合,可与点![]() 重合),满足
重合),满足![]() ,
,![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
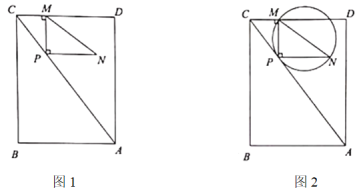
(1)若![]() ,则
,则![]() ___________;
___________;
(2)当点![]() 在
在![]() 的平分线上时,求
的平分线上时,求![]() 的长;
的长;
(3)当点![]() 的位置发生改变时:
的位置发生改变时:
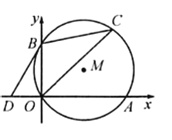
①如图2,![]() 的外接圆是否与
的外接圆是否与![]() 一直保持相切.说明理由;
一直保持相切.说明理由;
②直接写出![]() 的外接圆与
的外接圆与![]() 相切时
相切时![]() 的长.
的长.
【答案】(1)9;(2)![]() ;(3)①
;(3)①![]() 的外接圆与
的外接圆与![]() 一直保持相切,理由见解析;②4.
一直保持相切,理由见解析;②4.
【解析】
(1)根据平行线截线段成比例得到![]() ,求出
,求出![]() ,则
,则![]() ;
;
(2)根据平行线截线段成比例得到![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,再根据角的平分线上的点到角的两边的距离相等得到
,再根据角的平分线上的点到角的两边的距离相等得到![]() ,最后利用等面积法列出
,最后利用等面积法列出![]() 的方程,解方程得出x,最后代入
的方程,解方程得出x,最后代入![]() 即可得出答案;
即可得出答案;
(3)①根据直径所对的圆周角是直角,可知![]() 的外接圆是以
的外接圆是以![]() 的中点
的中点![]() 为圆心,
为圆心,![]() 为半径的圆;利用
为半径的圆;利用![]() 证出
证出![]() ,利用圆中半径相等,证出
,利用圆中半径相等,证出![]() ,即可得出答案;
,即可得出答案;
②当![]() 的外接圆与
的外接圆与![]() 相切时(图见解析),利用
相切时(图见解析),利用![]() ,
,![]() 表示出
表示出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再根据
,再根据![]() ,列出方程
,列出方程![]() ,解出
,解出![]() ,则
,则![]() .
.
解:(1)在矩形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
在矩形![]() 中,
中,![]()
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
故答案为:9.
(2)如图1,
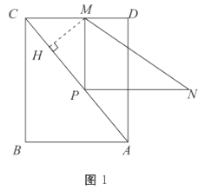
在矩形![]() 中,
中,![]()
∵![]() 于点
于点![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
作![]() 于点
于点![]() ,
,
∵点![]() 在
在![]() 的平分线上,
的平分线上,
∴![]() .
.
![]() ,
,
即![]() ,解得
,解得![]() .
.
∴![]() .
.
(3)①![]() 的外接圆与
的外接圆与![]() 一直保持相切.
一直保持相切.
如图2所示,
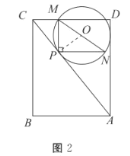
∵![]() 是直角三角形,
是直角三角形,
∴![]() 的外接圆是以
的外接圆是以![]() 的中点
的中点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,即
,即![]() .
.
∵点![]() 是
是![]() 斜边
斜边![]() 的中点,
的中点,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴当点![]() 的位置发生改变时,
的位置发生改变时,![]() 的外接圆与
的外接圆与![]() 一直保持相切.
一直保持相切.
②4.
如图3,
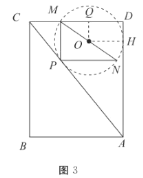
![]() 的外接圆与
的外接圆与![]() 切于点
切于点![]() 时,
时,
![]() 的外接圆是以
的外接圆是以![]() 的中点
的中点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
四边形![]() 为矩形,
为矩形,![]() .
.
设![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() .
.
∴当![]() 的外接圆与
的外接圆与![]() 相切时,
相切时,![]() 的长为4.
的长为4.

【题目】某中学开展普通话演讲比赛,九(1)、(2)两个班根据初赛成绩各选出5名选手参加复赛,10名选手的复赛成绩如图所示:
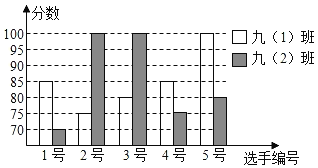
(1)根据如图补充完成下面的成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
九(1)班 | 85 |
| 85 |
|
| 60% |
九(2)班 | 85 | 80 |
| 160 | 100% |
|
(2)九(1)班学生说他们的复赛成绩好于九(2)班,结合图表,请你给出三条支持九(1)班学生观点的理由.
(3)如果从复赛成绩100分的3名选手中任选2人参加学校决赛,求选中的两位选手恰好一位来自于九(1)班,另一位来自于九(2)班的概率.