题目内容
 直线y=-x+4与x轴交于点A,与y轴交于点B,点P是线段AB上的动点,Q为线段OP上的中点,则⊙Q的面积不可能是
直线y=-x+4与x轴交于点A,与y轴交于点B,点P是线段AB上的动点,Q为线段OP上的中点,则⊙Q的面积不可能是
- A.5π
- B.4π
- C.3π
- D.2π
A
分析:由一次函数的解析式可求出函数和坐标轴交点的坐标,因为Q为线段OP上的中点,则OP是圆Q的直径,求出OP的最小值和最大值,也就是求出了圆Q的面积的最值,有其取值范围再做选择即可.
解答:设y=0.则0=-x+4,
∴x=4,
∴A的坐标为(4,0),
∴OA=4,
设x=0.则y=4,
∴OB=4,
∴AB= =4
=4 ,
,
∵点P是线段AB上的动点,
∴OP⊥AB时,OP最小为 AB=2
AB=2 ,
,
∵Q为线段OP上的中点,
∴此时⊙Q的面积=π( )2=2π,
)2=2π,
∵点P是线段AB上的动点,
∴当点P和A或B重合时,OP最大为4,
∴此时⊙Q的面积=π×22=4π,
∴2π<⊙Q的面积<4π,
故选A.
点评:本题考查了一次函数和坐标轴交点的问题、直角三角形的性质:斜边上的中线等于斜边的一半以及勾股定理的运用,解题的关键是求出圆Q的最大值和最小值.
分析:由一次函数的解析式可求出函数和坐标轴交点的坐标,因为Q为线段OP上的中点,则OP是圆Q的直径,求出OP的最小值和最大值,也就是求出了圆Q的面积的最值,有其取值范围再做选择即可.
解答:设y=0.则0=-x+4,
∴x=4,
∴A的坐标为(4,0),

∴OA=4,
设x=0.则y=4,
∴OB=4,
∴AB=
 =4
=4 ,
,∵点P是线段AB上的动点,
∴OP⊥AB时,OP最小为
 AB=2
AB=2 ,
,∵Q为线段OP上的中点,
∴此时⊙Q的面积=π(
 )2=2π,
)2=2π,∵点P是线段AB上的动点,
∴当点P和A或B重合时,OP最大为4,
∴此时⊙Q的面积=π×22=4π,
∴2π<⊙Q的面积<4π,
故选A.
点评:本题考查了一次函数和坐标轴交点的问题、直角三角形的性质:斜边上的中线等于斜边的一半以及勾股定理的运用,解题的关键是求出圆Q的最大值和最小值.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 内作Rt△ABC,∠BAC=90°.
内作Rt△ABC,∠BAC=90°.
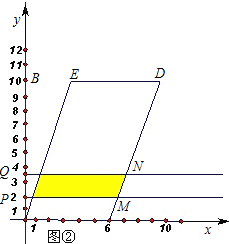
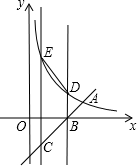 过B、C分别作y轴的平行线交双曲线
过B、C分别作y轴的平行线交双曲线 (2012•鄂州)直线y=-
(2012•鄂州)直线y=- (2013•威海)如图,在平面直角坐标系中,直线y=
(2013•威海)如图,在平面直角坐标系中,直线y=