题目内容
某M种水果一上市,立刻赢得市民的喜欢,水果店的小李就用3000元购进了一批这种水果,前两天以高于进价40%的价格共卖出150kg,第三天她发现市场上这种水果量陡增,而自己的M种水果卖相已不大好,于是果断地将剩余这种水果以低于进价20%的价格全部售出,前后一共获利750元(获利=售价-进价),求小李所进M种水果的数量.
考点:分式方程的应用
专题:
分析:设这批水果的数量有x千克,则水果的进价为
元,根据售价-进价=利润建立方程求出其解就可以求出结论
| 3000 |
| x |
解答:解:设这批水果的数量有x千克,则水果的进价为
元,由题意,得
150×
(1+40%)+(x-150)×
×(1-20%)-300=750,
解得:x=200.
经检验,x=200是原方程的解.
答:小李所进M种水果的数量是200千克.
| 3000 |
| x |
150×
| 3000 |
| x |
| 3000 |
| x |
解得:x=200.
经检验,x=200是原方程的解.
答:小李所进M种水果的数量是200千克.
点评:本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,销售问题的数量关系获利=售价-进价的运用,解答时由销售问题的数量关系建立方程是关键.

练习册系列答案
相关题目
一元二次方程x2+2x=0的根是( )
| A、x=0 |
| B、x=-2 |
| C、x=0或x=-2 |
| D、x=0或x=2 |
一组数据:0,2,3,4,4,5的众数和中位数分别是( )
| A、3和4 | B、4和3 |
| C、3.5和4 | D、4和3.5 |
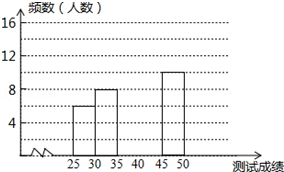 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: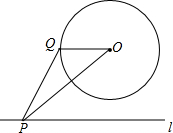 如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为
如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为