ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕФкЃЌЕу![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() дк
дк![]() жсе§АыжсЃЌЖЅЕу
жсе§АыжсЃЌЖЅЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсИКАыжсКЭе§АыжсЩЯЃЌ
жсИКАыжсКЭе§АыжсЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЃЈ1ЃЉЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂвдУПУы
ГіЗЂвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШби
ИіЕЅЮЛГЄЖШЕФЫйЖШби![]() ЯђжеЕу
ЯђжеЕу![]() дЫЖЏЃЌЕу
дЫЖЏЃЌЕу![]() дЫЖЏЕФЪБМфЮЊ
дЫЖЏЕФЪБМфЮЊ![]() ЃЌвд
ЃЌвд![]() ЮЊаББпдк
ЮЊаББпдк![]() гвБпЩЯЗНзїЕШбќжБНЧШ§НЧаЮ
гвБпЩЯЗНзїЕШбќжБНЧШ§НЧаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЩш
ЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЌЧѓ
ЃЉЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯпНЛ
ЕФДЙЯпНЛ![]() жсгк
жсгк![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕБЫФБпаЮ
ЃЌЕБЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЪБЃЌЧѓ
ЃЌЪБЃЌЧѓ![]() ЕФжЕМА
ЕФжЕМА![]() ЕузјБъЃЎ
ЕузјБъЃЎ
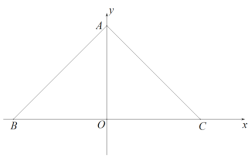
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉS=2tЃЈ0ЁмtЁм4ЃЉЃЛЃЈ3ЃЉQЃЈ0ЃЌ-2ЃЉЃЎ
ЃЛЃЈ2ЃЉS=2tЃЈ0ЁмtЁм4ЃЉЃЛЃЈ3ЃЉQЃЈ0ЃЌ-2ЃЉЃЎ
ЁОНтЮіЁП
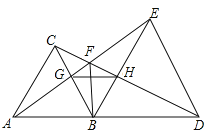
ЃЈ1ЃЉИљОнШ§НЧаЮУцЛ§ЙЋЪНЧѓЕУBCЕФГЄЃЌШЛКѓИљОнЕШбќШ§НЧаЮЕФаджЪЧѓOBЕФГЄЃЌДгЖјРћгУЙДЙЩЖЈРэЧѓНтЃЛ
ЃЈ2ЃЉзїPMЁЭBCгкNЃЌDHЁЭPCгкHЃЎРћгУЙДЙЩЖЈРэЧѓГіPCЕФГЄЃЈгУtБэЪОЃЉМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉзїPNЁЭyжсгкNЃЌDKЁЭPNгкKЃЌDHЁЭPCгкHЃЌСЌНгAHЁЂDHЃЎЪзЯШжЄУїAЁЂPЁЂDЁЂCЫФЕуЙВдВЃЌЭЦГіЁЯDAC=ЁЯDPC=45ЁуЃЌЁЯDAO=90ЁуЃЌгЩЁїPNQЁеЁїDKPЃЌПЩЕУDP=PQ=DCЃЌПЩЕУЫФБпаЮPQCDЪЧе§ЗНаЮЃЌИљОнЬтвтСаГіЗНГЬМДПЩНтОіЮЪЬтЃЛ
НтЃКЁп![]()
ЁрBC=8
гжЁп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() дк
дк![]() жсе§АыжсЃЌЖЅЕу
жсе§АыжсЃЌЖЅЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсИКАыжсКЭе§АыжсЩЯЃЌ
жсИКАыжсКЭе§АыжсЩЯЃЌ![]() ЃЌ
ЃЌ
ЁрOB=OC=![]() ЃЌ
ЃЌ
ЁрдкRtЁїOABжаЃЌ![]()
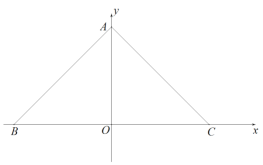
ЃЈ2ЃЉШчЭМ1жаЃЌзїDMЁЭXжсгкMЃЌPKЁЭDMгкKНЛyжсгкNЃЌDHЁЭPCгкHЃЌзїPEЁЭxжсгкEЃЌСЌНгAHЁЂDHЃЎ
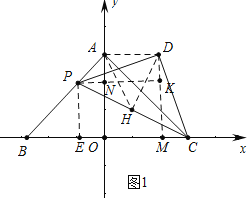
гЩЃЈ1ЃЉПЩжЊЃЌOA=OB=4
ЁрЁЯBAO=ЁЯCAO=45ЁуЃЌМДЁЯBAC=90Ёу
гжЁпЁїPCDЪЧЕШбќжБНЧШ§НЧаЮ
ЁрAH=DH=HP=HCЃЌ
ЁрAЁЂPЁЂDЁЂCЫФЕуЙВдВЃЌ
ЁрЁЯDAC=ЁЯDPC=45ЁуЃЌ
ЁрЁЯDAO=90ЁуЃЌ
ЁпЁЯDPK+ЁЯPDM=90ЁуЃЌЁЯPDM+ЁЯMDC=90ЁуЃЌ
ЁрЁЯDPK=ЁЯMDCЃЌ
ЁпЁЯPKD=ЁЯDMC=90ЁуЃЌDP=DCЃЌ
ЁрЁїPDKЁеЁїDCMЃЌ
ЁрPK=DM=OA=4ЃЌ
ЁпOA=OBЃЌЁЯAOB=90ЁуЃЌ
ЁрЁїAOBЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпPEЁЭBCЃЌ
ЁрЁЯPEB=90ЁуЃЌ
ЁрЁЯPBE=ЁЯBPE=45ЁуЃЌ
ЁпPB=![]() tЃЌ
tЃЌ
гЩЬтвтПЩжЊЃЌЫФБпаЮPEONЮЊОиаЮ
ЁрPE=BE=tЃЌON=4-tЃЌ
ЁрCM=DK=AN=OA=ON=OA-PE=4-tЃЌ
ЁрAD=4-ЃЈ4-tЃЉ=tЃЌ
ЁрS=![]()
![]() t4=2tЃЈ0ЁмtЁм4ЃЉЃЎ
t4=2tЃЈ0ЁмtЁм4ЃЉЃЎ
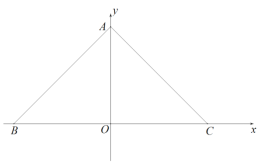
ЃЈ3ЃЉШчЭМ2жаЃЌ
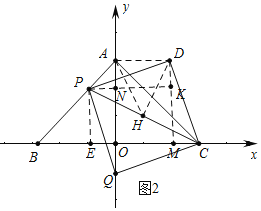
гЩЃЈ2ЃЉПЩжЊЃКPE=BE=tЃЌON=4-tЃЌCE=8-tЃЌ
дкRtЁїPCEжаЃЌPC2=t2+ЃЈ8-tЃЉ2=2t2-16t+64ЃЌ
ЁпЁїPDCЪЧЕШбќжБНЧШ§НЧаЮЃЌDHЁЭPCЃЌ
ЁрPH=CH=DHЃЌ
ЁрSЁїPDC=![]() =
=![]() ЃЈ0ЁмtЁм4ЃЉЃЎ
ЃЈ0ЁмtЁм4ЃЉЃЎ
взжЊAN=PN=DKЃЌЁЯQPN=ЁЯPDKЃЌЁЯPNQ=ЁЯPKD=90ЁуЃЌ
ЁрЁїPNQЁеЁїDKPЃЌ
ЁрDP=PQ=DCЃЌЁпPQЁЮDCЃЌ
ЁрЫФБпаЮPQCDЪЧЦНааЫФБпаЮЃЌ
ЁпЁЯDPQ=90ЁуЃЌ
ЁрЫФБпаЮPQCDЪЧОиаЮЃЌ
ЁпPD=PQЃЌ
ЁрЫФБпаЮPQCDЪЧе§ЗНаЮЃЌ
гЩЬтвтЃК2ЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌ
ЃЌ
2ЃЈ![]() ЃЉ=10t
ЃЉ=10t
ећРэЕУt2-8t+32=0ЃЌ
НтЕУЃКt=2Лђ16ЃЈЩсЦњЃЉЃЌ
Ёрt=2ЪБЃЌЫФБпаЮPDCQЕФУцЛ§ЮЊ20ЃЌ
ДЫЪБPC=2![]() ЃЌPQ=2
ЃЌPQ=2![]() ЃЌPN=2ЃЌON=2ЃЌNQ=
ЃЌPN=2ЃЌON=2ЃЌNQ=![]() =4ЃЌ
=4ЃЌ
ЁрOQ=QN-ON=2ЃЌ
ЁрQЃЈ0ЃЌ-2ЃЉЃЎ

 гХМгОЋОэЯЕСаД№АИ
гХМгОЋОэЯЕСаД№АИ