题目内容
一个机器零件的形状如图所示，已知Rt△ABC中，∠BAC=30°，BC=2.5cm，BD=13cm，AD=12cm，求△ABD的面积．考点：勾股定理,勾股定理的逆定理
专题：
分析：先根据直角三角形的性质求出AB的长，再由勾股定理的逆定理判断出△ABD的形状，根据三角形的面积公式即可得出结论．
解答：解：∵Rt△ABC中，∠BAC=30°，BC=2.5cm，
∴AB=2BC=5cm．
∵52+122=132，即AB2+AD2=BD2，
∴△ABD是直角三角形．
∴AB=2BC=5cm．
∵52+122=132，即AB2+AD2=BD2，
∴△ABD是直角三角形．
点评：本题考查的是勾股定理，直角三角形中，30°的角所对的直角边等于斜边的一半是解答此题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
下列哪组条件能判别四边形ABCD是平行四边形？（ ）| A、AB∥CD，AD=BC |
| B、AB=AD，CB=CD |
| C、∠A=∠B，∠C=∠D |
| D、AB=CD，AD=BC |
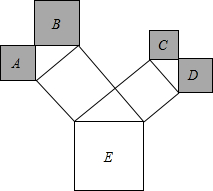如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是5，3，2，3，则最大正方形E的面积是
如图，学校准备建一个矩形花圃ABCD，已知花圃的一边靠墙（墙的最大可用长度为10m），其余用总长为36m的篱笆围成，且中间隔有一道篱笆（平行于AB）．设花圃的一边AB为xm，面积为ym2．
如图，该图形是立体图形