题目内容
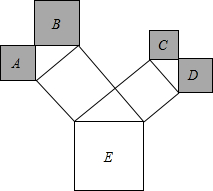 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是5,3,2,3,则最大正方形E的面积是
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是5,3,2,3,则最大正方形E的面积是考点:勾股定理
专题:
分析:分别设中间两个正方形和最大正方形的边长为x,y,z,由勾股定理得出x2=32+52,y2=22+32,z2=x2+y2,即最大正方形的面积为z2.
解答:解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,则由勾股定理得:
x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形E的边长为:
,所以面积为:z2=47.
故答案为:47.
x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形E的边长为:
| 47 |
故答案为:47.
点评:本题考查的是勾股定理,题中采用了设“中间变量法”如题中所示:分别由勾股定理求出x2,y2,再由勾股定理求出大正方形边长的平方z2=x2+y2,主要考查运用勾股定理解决实际问题的能力.

练习册系列答案
相关题目
下列各组线段能组成一个三角形的是( )
| A、3cm,3cm,6cm |
| B、2cm,3cm,6cm |
| C、5cm,8cm,12cm |
| D、4cm,7cm,11cm |
 ”、“
”、“ ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a b=a和a
b=a和a b=b,例如3
b=b,例如3  2=3,3
2=3,3 2=2.则(2014
2=2.则(2014 2013)
2013) (2012
(2012 2011)的值是
2011)的值是 如图,从电线杆离地面8米处向地面拉一条缆绳,这条缆绳在地面上的固定点距离电线杆底部15米,则这条缆绳的长为
如图,从电线杆离地面8米处向地面拉一条缆绳,这条缆绳在地面上的固定点距离电线杆底部15米,则这条缆绳的长为 一个机器零件的形状如图所示,已知Rt△ABC中,∠BAC=30°,BC=2.5cm,BD=13cm,AD=12cm,求△ABD的面积.
一个机器零件的形状如图所示,已知Rt△ABC中,∠BAC=30°,BC=2.5cm,BD=13cm,AD=12cm,求△ABD的面积.


