题目内容
如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为________．
3
分析：首先，利用等边三角形的性质求得AD=3；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD．
解答：如图，∵在等边△ABC中，∠B=60°，AB=6，D是BC的中点，
∴AD⊥BD，∠BAD=∠CAD=30°，
∴AD=ABcos30°=6×
=3．
根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE，
∴∠DAE=∠EAC+∠CAD=∠EAC+∠BAD=60°，
∴△ADE的等边三角形，
∴DE=AD=3，即线段DE的长度为3．
故答案是：3．
点评：本题考查了旋转的性质、等边三角形的性质．旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．
分析：首先，利用等边三角形的性质求得AD=3
；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD．解答：如图，∵在等边△ABC中，∠B=60°，AB=6，D是BC的中点，
∴AD⊥BD，∠BAD=∠CAD=30°，
∴AD=ABcos30°=6×
=3．根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE，
∴∠DAE=∠EAC+∠CAD=∠EAC+∠BAD=60°，
∴△ADE的等边三角形，
∴DE=AD=3
，即线段DE的长度为3．故答案是：3
．点评：本题考查了旋转的性质、等边三角形的性质．旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
16、如图，在等边△ABC的边BC上任取一点D，作∠ADE=60°，DE交∠C的外角平分线于E，则△ADE是
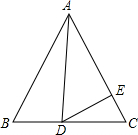如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
21、如图，在等边△ABC中，AD是∠BAC的平分线，点E在AC边上，且∠EDC=15°．
如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE=CD，AB=10cm．
如图，在等边△ABC中，BF是高，D是BF上一点，且OF=AF，作OE⊥BF，垂足为D，且OE=OB，连AE、AO、BE，求证：