Question

2．如图，抛物线y=a（x-1）²+h的顶点为M，与x轴正半轴交于点C，直线$y=\frac{3}{4}x+\frac{3}{2}$与抛物线交于点A（2，3），与x轴交于点B，且AB=BC．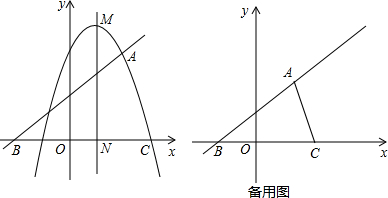

（1）求抛物线的函数关系式；
（2）若抛物线对称轴与x轴交于点N，P为直线AB上一点，过点P作MN的平行线交抛物线于点Q，问：以M、N、P、Q四点为顶点构成的四边形能否为等腰梯形？若能，求点P的坐标；若不能，请说明理由；
（3）将抛物线作适当平移，顶点M落在直线AB上，与x轴交于D、E两点，是否存在这样的抛物线，使得△MDE∽△BAC？若存在请求出平移后的抛物线的解析式；若不存在，请说明理由．

Answer 1

分析 （1）先求出点B坐标，进一步求出AB的长度，之后求出点C坐标，代入抛物线求解即可；
（2）设出点P，Q的坐标，运用坐标表示相应线段长度，根据等腰梯形的相关性质建立方程，求解；
（3）首先根据顶点在直线AB上设出点M的坐标，进一步表示抛物线解析式，求出点D，E的坐标，根据相似建立方程求解即可．

解答 解：（1）直线y=$\frac{3}{4}x+\frac{3}{2}$，令y=0，解得：x=-2，
∴点B（-2，0），
由A（2，3），可求AB=$\sqrt{（2+2）^{2}+（3-0）^{2}}$=5，
∴BC=AB=5，
∵点B（-2，0），
∴点C（3，0），
∵y=a（x-1）²+h过点A（2，3），点C（3，0），
∴$\left\{\begin{array}{l}{3=a+h}\\{0=4a+h}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-1}\\{h=4}\end{array}\right.$，
所以抛物线的解析式为：y=-（x-1）²+4=-x²+2x+3，
（2）如图1：

y=-x²+2x+3的对称轴：x=1，顶点M（1，4），
由点P在直线AB上，设点P（m，$\frac{3}{4}m+\frac{3}{2}$），则点Q（m，-m²+2m+3），
根据等腰三角形性质可得：4-（-m²+2m+3）=$\frac{3}{4}m+\frac{3}{2}$，
解得：m=2（舍去），或m=$\frac{3}{4}$，
此时：$\frac{3}{4}m+\frac{3}{2}$的值为：$\frac{33}{16}$，
以M、N、P、Q四点为顶点构成的四边形能为等腰梯形，点P的坐标：（$\frac{3}{4}$，$\frac{33}{16}$）；
（3）如图2：连接MD，ME，过点M作MG⊥x轴，过点A作AH⊥x轴，

设点M（n，$\frac{3}{4}n+\frac{3}{2}$），则抛物线的解析式：y=$-（x-n）^{2}+\frac{3}{4}n+\frac{3}{2}$，
令y=0，得：0=$-（x-n）^{2}+\frac{3}{4}n+\frac{3}{2}$，
解得：x=n+$\frac{\sqrt{3n+6}}{2}$，或x=n-$\frac{\sqrt{3n+6}}{2}$，
∴点D（n-$\frac{\sqrt{3n+6}}{2}$，0），
∴DG=n-（n-$\frac{\sqrt{3n+6}}{2}$）=$\frac{\sqrt{3n+6}}{2}$，
由点A（2，3），点C（3，0），可得：AH=3，DH=3-2=1，
∴tan∠ACH=3，
要使得△MDE∽△BAC，有：∠MDH=∠ACH，
∴tan∠MDG=3，$\frac{MG}{DG}$=3，
∴$\frac{3}{4}n+\frac{3}{2}$=$\frac{\sqrt{3n+6}}{2}$×3，
解得：n=10，或n=-2（舍去），
∴点M（10，9），
所以此时抛物线的解析式为：y=-（x-1）²+9．

点评 此题主要考查二次函数的综合问题，会求函数图象与轴的交点，会运用点求解析式，知道设点坐标表示线段，寻找关系列出方程并准确求解是解题的关键．