题目内容
7. 如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.此时BE=DE,若AB=4,AD=8,求△BDE的面积.
如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.此时BE=DE,若AB=4,AD=8,求△BDE的面积.
分析 设AE=x,则BE=DE=8-x,在直角△ABE中利用勾股定理即可列方程求得x的值,然后根据三角形面积公式求解.
解答 解:设AE=x,则BE=DE=8-x,
在直角△ABE中,AB2+AE2=BE2,
即42+x2=(8-x)2,
解得:x=3,
则AE=3,DE=8-3=5,
则S△BDE=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×4×(8-3)=10.
点评 本题考查了图形的折叠以及勾股定理,正确利用勾股定理求得AE的长是解决本题的关键.

练习册系列答案
相关题目
12.如图所示图形是轴对称图形的有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.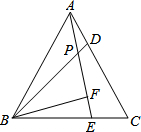 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )| A. | 2 | B. | 3 | C. | 1 | D. | 2$\sqrt{3}$ |
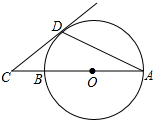 如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=
如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=