题目内容
【题目】如图1,![]() 直线
直线![]() 分别交
分别交![]() 于点
于点![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() 与
与![]() 交于点
交于点![]() 交
交![]() 于
于![]() .
.

(1)求证:![]()
(2)如图2,连接![]() 为
为![]() 上一动点,
上一动点,![]() 平分
平分![]() 交
交![]() 于
于![]() 则
则![]() 的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
【答案】(1)详见解析;(2)![]() 的大小不发生变化,一直是
的大小不发生变化,一直是![]() .
.
【解析】
(1)利用平行线的性质推知![]() ;然后根据角平分线的性质、三角形内角和定理证得
;然后根据角平分线的性质、三角形内角和定理证得![]() ,即
,即![]() ,故结合已知条件
,故结合已知条件![]() ,易证
,易证![]() ;
;
(2)利用三角形外角定理、三角形内角和定理求得![]() ;然后由邻补角的定义、角平分线的定义推知
;然后由邻补角的定义、角平分线的定义推知![]() ;最后根据图形中的角与角间的和差关系求得
;最后根据图形中的角与角间的和差关系求得![]() 的大小不变,是定值
的大小不变,是定值![]() .
.
解:(1)证明:如图1,
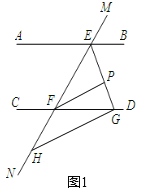
![]() ,
,
![]() .
.
又![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,
![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() ;
;
(2)![]() 的大小不发生变化,理由如下:
的大小不发生变化,理由如下:
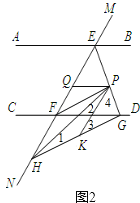
如图2,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
∴![]() ,
,
∴![]() 的大小不发生变化,一直是
的大小不发生变化,一直是![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).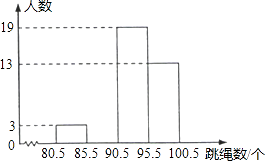
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.