题目内容
(1)计算:|-
|+2-1+(π-
)0-tan60°
(2)解方程:
①(x-2)2=16
②x2-5x+6=0.
| 3 |
| 3 |
(2)解方程:
①(x-2)2=16
②x2-5x+6=0.
考点:解一元二次方程-因式分解法,实数的运算,零指数幂,负整数指数幂,解一元二次方程-直接开平方法,特殊角的三角函数值
专题:计算题
分析:(1)根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=
+
+1-
,然后合并即可;
(2)①利用直接开平方法解方程;
②利用因式分解法解方程.
| 3 |
| 1 |
| 2 |
| 3 |
(2)①利用直接开平方法解方程;
②利用因式分解法解方程.
解答:解:(1)原式=
+
+1-
=
;
(2)①x-2=±4,
所以x1=6,x2=-2;
②(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3.
| 3 |
| 1 |
| 2 |
| 3 |
=
| 3 |
| 2 |
(2)①x-2=±4,
所以x1=6,x2=-2;
②(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3.
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了实数的运算.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
若|a|=9,|b|=4,且a+b>0,那么a-b值为( )
| A、5或-5 | B、13或-13 |
| C、5或13 | D、5或-13 |
下列各式中运算正确的是( )
| A、-3a-3a=0 |
| B、a4×a4=a16 |
| C、3a2+2a2=5a2 |
| D、3(a-2b)=3a-2b |
要使分式
有意义,x的取值范围为( )
| ||
| x+5 |
| A、x≠-5 | B、x>0 |
| C、x≠-5且x>0 | D、x≥0 |
 如图,两建筑物的水平距离BC是30米,从A点测得D点的俯角α是35°,测得点C的俯角β为43°,求这两座建筑物的高度.(计算过程中的结果均保留整数)
如图,两建筑物的水平距离BC是30米,从A点测得D点的俯角α是35°,测得点C的俯角β为43°,求这两座建筑物的高度.(计算过程中的结果均保留整数) 如图,点C是线段AB的一个三等分点,D在CB上,CD:DB=9:1,且CD-AC=2,求线段AB的长.
如图,点C是线段AB的一个三等分点,D在CB上,CD:DB=9:1,且CD-AC=2,求线段AB的长. 如图,线段AB的长为8cm,点C为线段AB任意一点,点M为线段AC的中点,点N为线段BC的中点.
如图,线段AB的长为8cm,点C为线段AB任意一点,点M为线段AC的中点,点N为线段BC的中点.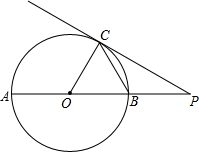 如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.
如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.