Question

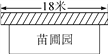
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米(如图所示)，设这个苗圃园垂直于墙的一边的长为x米．

(1)若苗圃园的面积为72平方米，求x的值；

(2)若平行于墙的一边长不大于14米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；

(3)当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．

Answer 1

【答案】(1) x＝12；(2)平行于墙的一边长为14米时，这个苗圃园的面积最大，为112平方米；(3) 6≤x≤10.

【解析】试题分析: （1）根据题意得方程求解即可,（2）设苗圃园的面积为y,根据题意得到二次函数解析式y＝x(30－2x)＝－2x2＋30x,根据二次函数的性质求解即可,（3）由题意得不等式,即可得到结论．

试题解析:(1)根据题意得(30－2x)x＝72,解得x＝3或12.

∵30－2x≤18,∴x≥6,∴x＝12,

(2)设苗圃园的面积为y平方米,

∴y＝x(30－2x)＝－2x2＋30x＝－2＋112.5,

由题意知30－2x≤14,∴x≥8,

由(1)知x≥6,∴x≥8.

∵－2<0,∴当x>时,y随x的增大而减小,

又∵x≥8∴当x＝8时,y取最大值,y最大＝－2×82＋30×8＝112,

即平行于墙的一边长为30－2×8＝14(米)时,这个苗圃园的面积最大,为112平方米,

(3)由题意得－2x2＋30x≥100,解得5≤x≤10.

由(1)知x≥6,∴6≤x≤10.