Question

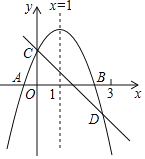
【题目】如图，在平面直角坐标系中，已知抛物线y＝ax2＋bx－5与x轴交于A(－1，0)，B(5，0)两点，与y轴交于点C，连接AC，BC.

(1)求抛物线的函数表达式；

(2)若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标．

Answer 1

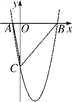
【答案】（1）y＝x2－4x－5（2）点D的坐标为(0，1)或（0， ）.

【解析】试题分析：（1）根据待定系数法直接抛物线解析式；

（2）分两种情况，利用相似三角形的比例式即可求出点D的坐标.

试题解析：(1)∵点A(－1，0)，B(5，0)在抛物线y＝ax2＋bx－5上，

∴

∴

∴抛物线的表达式为y＝x2－4x－5；

(2)令x＝0，y＝－5，

∴C(0，－5)，

∴OC＝OB，

∴∠OBC＝∠OCB＝45°.

∵OA＝1，OB＝5，

∴AB＝6，BC＝5，

.要使以B，C，D为顶点的三角形与△ABC相似，

则有或，

如图：

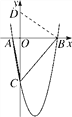
①当时，CD＝AB＝6，

∴D(0，1)；

②当时，

∴，

∴CD＝，

∴D.综上所述，点D的坐标为(0，1)或.