题目内容
6.已知y+2与2x-3成正比例,且x=3时y=4.(1)求y与x之间的函数关系式;
(2)当y=1时,求x的值.
(3)求此函数与坐标轴围成的三角形的面积.
分析 (1)先设出函数的解析式为y+2=k(2x-3),再将x=3,y=4代入即可求得函数的关系式.
(2)把y=1代入求得的解析式求得即可;
(3)求得与坐标轴的交点坐标,然后根据三角形面积公式求得即可.
解答 解:(1)设y+2=k(2x-3),
把x=3,y=4代入得4+2=k(6-3),
解得k=2,
∴y+2=2(2x-3),
∴y=4x-8;
(2)把y=1代入y=4x-8得1=4x-8,
解得$x=\frac{9}{4}$;
(3)令x=0,则y=-8,
∴此函数与y轴交于(0,-8),
令y=0,则0=4x-8,
解得x=2,
∴此函数与x轴交于(2,0),
∴S=$\frac{1}{2}$×8×2=8.
点评 本题考查了待定系数法求一次函数的解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
17.在2,0,-2,-3这四个数中,最小的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
11.抛物线y=2x2-4x+5的对称轴是( )
| A. | x=2 | B. | x=-1 | C. | x=-2 | D. | x=1 |
18.若2x+3y=3,则4x•8y=( )
| A. | 8 | B. | 6 | C. | 9 | D. | 90° |
15. 如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
 如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )| A. | 24cm2 | B. | 18cm2 | C. | 12cm2 | D. | 30cm2 |
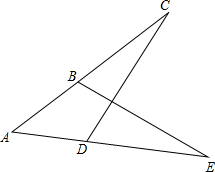 如图,AD=AB,∠C=∠E,AB=3,AE=8.则DE=5.
如图,AD=AB,∠C=∠E,AB=3,AE=8.则DE=5.