Question

【题目】如图，在矩形 ABCD 中AB=8，AD=10，点 E 是 CD 的中点，将这张纸片依次折叠两次： 第一次折叠纸片使点 A 与点 E 重合，如图 2，折痕为 MN，连接 ME、NE；第二次折叠纸片使点 N 与点 E 重合，如图 3，点 B 落到 B′处，折痕为 HG，连接 HE，则下列结论正确的个数是（ ）①ME∥HG；②△MEH 是等边三角形；③∠EHG=∠AMN；④tan∠EHG=；

A.1 个B.2 个C.3 个D.4 个

Answer 1

【答案】C

【解析】

根据折叠的性质可得M//GH，再根据等量代换，即可得出∠AMN=∠EHG；在直角三角形中运用勾股定理，即可得出AM=EM=7.4，再根据相似三角形的性质，即可得出EN=7、5=AN，进而得到，最后根据∠EMH≠60°，可得AMEH不是等边三角形.

解：如图3，由折叠可得，∠MEN=∠A=90°，HG⊥NE，

即ME⊥EN，HG⊥EN，

∴EM//GH，故①正确；

∴∠NME=∠NHG，

由折叠可得，∠NME=∠AMV，∠EHG=∠NHG，

∴∠AMN=∠EHG，故③正确；

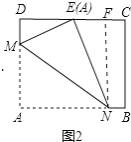
如图2，作NF⊥CD于F.

设DM=x，则AM=EM=10-x，

∵点E是CD的中点，AB=CD= ，

∴DE=CD=，

在Rt△DEM中，

∵

∴，解得x=2.6，

∴DM=2.6，AM=EM=7.4，

∵∠DEM+∠NEF=90°，∠NEF+∠ENH=90°，

∴∠DEM=∠ENF，

∵∠D=∠EFN=90°，

，

，

，故④正确；

又 ，

∴ ，即，

不是等边三角形，故②错误．

正确的结论有3个．

故选：C．