题目内容
 如图,以正方形ABCD的对角线BD为边作菱形BEFD,则∠BDF是∠F的
如图,以正方形ABCD的对角线BD为边作菱形BEFD,则∠BDF是∠F的考点:正方形的性质,含30度角的直角三角形,菱形的性质
专题:
分析:连接AC与BD相交于O,过点E作EH⊥BD于H,可得四边形OCEH是矩形,根据矩形的对边相等可得EH=OC,再根据菱形的四条边都相等可得BD=BE,然后求出EH=
BE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠DBE=30°,然后根据菱形的对角相等求出∠F,邻角互补求出∠BDF,再计算即可得解.
| 1 |
| 2 |
解答: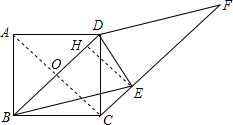 解:如图,连接AC与BD相交于O,过点E作EH⊥BD于H,
解:如图,连接AC与BD相交于O,过点E作EH⊥BD于H,
∵四边形ABCD是正方形,四边形BEFD是菱形,
∴AC⊥BD,BD∥CF,
∴四边形OCEH是矩形,
∴EH=OC=
AC=
BD,
∵四边形BEFD是菱形,
∴BD=BE,
∴EH=
BE,
∴∠DBE=30°,
∵四边形BEFD是菱形,
∴∠F=∠DBE=30°,
∠BDF=180°-∠DBE=180°-30°=150°,
∴∠BDF是∠F的5倍.
故答案为:5.
 解:如图,连接AC与BD相交于O,过点E作EH⊥BD于H,
解:如图,连接AC与BD相交于O,过点E作EH⊥BD于H,∵四边形ABCD是正方形,四边形BEFD是菱形,
∴AC⊥BD,BD∥CF,
∴四边形OCEH是矩形,
∴EH=OC=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形BEFD是菱形,
∴BD=BE,
∴EH=
| 1 |
| 2 |
∴∠DBE=30°,
∵四边形BEFD是菱形,
∴∠F=∠DBE=30°,
∠BDF=180°-∠DBE=180°-30°=150°,
∴∠BDF是∠F的5倍.
故答案为:5.
点评:本题考查了正方形的性质,矩形的判定与性质,菱形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,作辅助线构造出矩形的和含30°角的直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程2x2+3x=0解是( )
| A、x1=0,x2=-3 | ||
B、x1=0,x2=
| ||
C、x1=0,x2=-
| ||
D、x1=0,x2=-
|
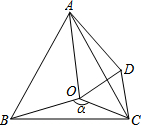 如图,已知点O是等边AO=AD内一点,∠BOC=α,且OC=3.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,则OD=
如图,已知点O是等边AO=AD内一点,∠BOC=α,且OC=3.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,则OD= 已知抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,2)三点.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,2)三点.