题目内容
4.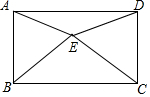 已知:如图,点E为矩形ABCD内一点,且EB=EC,则EA=ED(填“>”“<”或“=”)
已知:如图,点E为矩形ABCD内一点,且EB=EC,则EA=ED(填“>”“<”或“=”)
分析 根据矩形的对边相等和4个角都是90°的性质可得AB=CD,∠ABC=∠BCD,由EB=EC,可得∠EBC=∠ECB,那么∠ABE=∠ECD,所以△ABE≌△DCE,进而可得AE=ED.
解答 解:解:∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠BCD,
∵EB=EC,
∴∠EBC=∠ECB,
∴∠ABE=∠ECD,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠DCE}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE,
∴AE=ED.
故答案为=.
点评 本题考查矩形的性质:对边相等、4个角都是90°,等角的余角相等,等边对等角,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.已知点M(a,3),点N(2,b)关于y轴对称,则(a+b)2015的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
13.巴黎与北京的时差为-7小时(正数表示同一时刻比北京时间早的时数),如果北京时间11月11日14:00,那么巴黎时间是( )
| A. | 11月11日21时 | B. | 11月11日7时 | C. | 11月10日7时 | D. | 11月11日5时 |
14.一个正数的两个平方根分别是2a-1与-a+2,则a的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
 一次函数y=kx+b的图象如图所示,若y>0,则x的取值范围是x<-2.
一次函数y=kx+b的图象如图所示,若y>0,则x的取值范围是x<-2. 如图,在扇形AOB中,∠AOB=90°,OA=OB=6,点C在OA上,将△BOC沿BC翻折,点O恰好落在$\widehat{AB}$上的D点处,则图中阴影部分的面积为9π-12$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,OA=OB=6,点C在OA上,将△BOC沿BC翻折,点O恰好落在$\widehat{AB}$上的D点处,则图中阴影部分的面积为9π-12$\sqrt{3}$.