Question

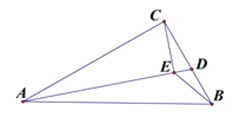
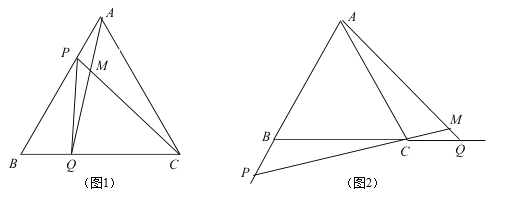
【题目】如图（1），点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都是1cm/s

（1）设运动时间是t，则当t=__________s时，△PBQ是直角三角形．

（2）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ的大小变化吗？若变化，则说明理由，若不变，则求出它的度数；

（3）如图（2），若P，Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ的大小变化吗？若变化，则说明理由，若不变，则求出它的度数．

Answer 1

【答案】（1）或；（2）不变，60°；（3）不变，120°

【解析】

（1）由题意得出AP＝BQ＝t，PB＝4﹣t，分∠PQB＝90°和∠BPQ＝90°两种情况进行求解；

（2）根据等边三角形的性质证明，即可求得∠BAQ＝∠ACP，再利用三角形外角的性质可证得∠CMQ＝60°；

（3）通过证明△PBC≌△QCA得出，利用三角形的内角和定理得出，进而求解．

解：（1）∵运动时间为ts，则AP＝BQ＝t，

∴PB＝4﹣t，

当∠PQB＝90°时，

∵∠B＝60°，

∴PB＝2BQ，

∴4﹣t＝2t，

解得，t＝，

当∠BPQ＝90°时，

∵∠B＝60°，

∴BQ＝2PB，

∴，

解得，t＝，

∴当t为s或s 时，△PBQ为直角三角形；

故答案为：或；

（2）不变，，

正△ABC中，，，，

，

，

，

∴在P、Q运动的过程中，∠CMQ不变，∠CMQ＝60°；

（3）不变，，

在正△ABC中，，，

，又由条件得，

∴△PBC≌△QCA（SAS），

，

又，

．

∴在P、Q运动的过程中，∠CMQ的大小不变，∠CMQ＝120°．