题目内容
10.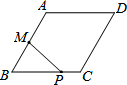 如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )| A. | 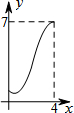 | B. | 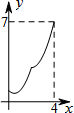 | C. | 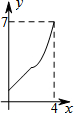 | D. | 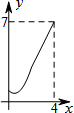 ? ? |
分析 分三种情况:(1)当0≤x≤$\frac{1}{2}$时,(2)当$\frac{1}{2}$<x≤2时,(3)当2<x≤4时,根据勾股定理列出函数解析式,判断其图象即可求出结果.
解答 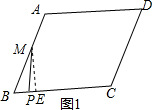 解:(1)当0≤x≤$\frac{1}{2}$时,
解:(1)当0≤x≤$\frac{1}{2}$时,
如图1,过M作ME⊥BC与E,
∵M为AB的中点,AB=2,
∴BM=1,
∵∠B=60°,
∴BE=$\frac{1}{2}$,ME=$\frac{\sqrt{3}}{2}$,PE=$\frac{1}{2}$-x,
在Rt△BME中,由勾股定理得:MP2=ME2+PE2,
∴y=${(\frac{\sqrt{3}}{2})}^{2}$${+(\frac{1}{2}-x)}^{2}$=x2-x+1;
(2)当$\frac{1}{2}$<x≤2时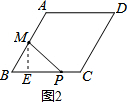
如图2,过M作ME⊥BC与E,
由(1)知BM=1,∠B=60°,
∴BE=$\frac{1}{2}$,ME=$\frac{\sqrt{3}}{2}$,PE=x-$\frac{1}{2}$,
∴MP2=ME2+PE2,
∴y=${(\frac{\sqrt{3}}{2})}^{2}$${+(\frac{1}{2}-x)}^{2}$=x2-x+1;
(3)当2<x≤4时,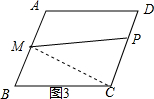
如图3,连结MC,
∵BM=1,BC=AB=2,∠B=60°,
∴∠BMC=90°,MC=$\sqrt{{2}^{2}-1}$=$\sqrt{3}$,
∵AB∥DC,
∴∠MCD=∠BMC=90°,
∴MP2=MC2+PC2,
∴y=${(\sqrt{3})}^{2}{+(x-2)}^{2}$=x2-4x+7;综合(1)(2)(3),只有B选项符合题意.
故选B.
点评 本题考查了动点问题的函数图象,勾股定理,正确的理解题意,画出图形是解题的关键.

练习册系列答案
相关题目
20.化简-16(x-0.5)的结果是( )
| A. | -16x-0.5 | B. | -16x+0.5 | C. | 16x-8 | D. | -16x+8 |
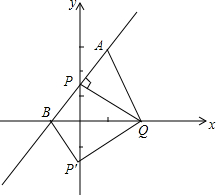 如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′
如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′
 如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上.
如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上.