题目内容
如图，某校实践活动小组在楼CD的最高点D处，测得楼AE的最高点A的仰角为30°，然后他们从楼CD的底部点C处，又测得楼AE上点B的仰角为10°．已知楼AE与楼CD之间的距离为CE，且AB=CE=30m，求楼CD的高度（结果精确到1m）．参考数据：
≈1.73，sin10°≈0.17，cos10°≈0.98，tan10°≈0.18．
解：作DF⊥AE，则CD=EF，DF=CE=30米．在Rt△BEC中，
，∴BE=30×tan10°≈30×0.18=5.4，
在Rt△DAF中，
，∴
，∴EF=AB+BE-AF=30+5.4-17.3=18.1≈18，
∴CD=18米．
答：楼CD的高度为18米．
分析：首先构造直角三角形，在构造的直角三角形中分别利用锐角三角函数值求得AB、BE、AF的长，用AB+BE-AF即可得到CD的长．
点评：本题考查了解直角三角形中的仰俯角问题，解决此类题目的关键是弄清有关的直角三角形中的有关角的度数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
李明对某校九年级（2）班进行了一次社会实践活动调查，从调查的内容中抽出两项．
调查一：对小聪、小亮两位同学的毕业成绩进行调查，其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算，计算的方法按4：4：2进行，毕业成绩达80分以上（含80分）为“优秀毕业生”，小聪、小亮的三项成绩如右表：（单位：分）
调查二：对九年级（2）班50名同学某项跑步成绩进行调查，并绘制了一个不完整的扇形统计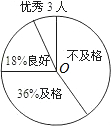图，
如图．
请你根据以上提供的信息，解答下列问题：
（1）小聪和小亮谁能达到“优秀毕业生”水平哪位同学的毕业成绩更好些？
（2）升入高中后，请你对他俩今后的发展给每人提一条建议；
（3）扇形图中“优秀率”是多少？
（4）“不及格”在扇形图中所占的圆心角是多少度？
（5）请从扇形图中，写出你发现的一个现象并分析其产生的原因．
调查一：对小聪、小亮两位同学的毕业成绩进行调查，其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算，计算的方法按4：4：2进行，毕业成绩达80分以上（含80分）为“优秀毕业生”，小聪、小亮的三项成绩如右表：（单位：分）
调查二：对九年级（2）班50名同学某项跑步成绩进行调查，并绘制了一个不完整的扇形统计图，
如图．| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
（1）小聪和小亮谁能达到“优秀毕业生”水平哪位同学的毕业成绩更好些？
（2）升入高中后，请你对他俩今后的发展给每人提一条建议；
（3）扇形图中“优秀率”是多少？
（4）“不及格”在扇形图中所占的圆心角是多少度？
（5）请从扇形图中，写出你发现的一个现象并分析其产生的原因．
21、某校九年级同学在一次数学实践活动中，去测量学校的树高，小明这一组的测量方法如下：如图，在B处竖一标杆AB，已知标杆AB=2.5m，小明站在点F处，眼睛E目测标杆顶部A与树顶C正好在同一视线上，（点F，B，D也在同一直线上）．这一组其他同学量得标杆到树的水平距离BD=3.6m，小明到标杆的水平距离FB=2m，小明的目高（眼睛到脚底的距离）EF=1.5m．根据这些数据，小明这一组同学很快就求出了树CD的高度．你会吗？请写出解答过程．
19、我区某校七年级（1）班周末组织学生进行创新素质实践“活动”，参观了如图中的一些景点和设施，为了便于确定方位，带队老师在图中建立了平面直角坐标系．（横轴和纵轴均为小正方形的边所在直线，每个小正方形边长为1个单位长度）
在某校组织的社会实践活动中，小明同学到某超市进行了一项社会调查，发现有一种水果1-6月份售价y（元/kg）与时间t（月）的关系可用一条线段上的点来表示，如图所示，该水果的成本m（元/kg）与时间t（月）满足二次函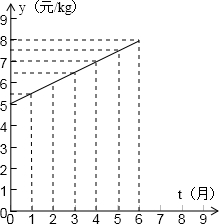
数关系，相应的数据如表所示．根据图象提供的信息，解答下列问题：
（1）求售价y（元/kg）与时间t（月）之间的函数关系式．
（2）求表中成本m（元/kg）与时间t（月）之间的函数关系式．
（3）你能求出每千克水果的利润W（元/kg）与时间t（月）之间的函数关系式吗？若该超市在1-6月份每月都销售水果3000kg，请问一个月内最多获利多少元？
数关系，相应的数据如表所示．根据图象提供的信息，解答下列问题：（1）求售价y（元/kg）与时间t（月）之间的函数关系式．
（2）求表中成本m（元/kg）与时间t（月）之间的函数关系式．
（3）你能求出每千克水果的利润W（元/kg）与时间t（月）之间的函数关系式吗？若该超市在1-6月份每月都销售水果3000kg，请问一个月内最多获利多少元？
| t（月） | 1 | 2 | 3 | … | ||||
| m（元/kg） |
|
|
3 | … |
