题目内容
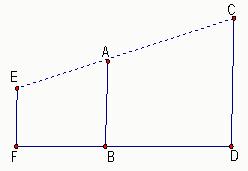
21、某校九年级同学在一次数学实践活动中，去测量学校的树高，小明这一组的测量方法如下：如图，在B处竖一标杆AB，已知标杆AB=2.5m，小明站在点F处，眼睛E目测标杆顶部A与树顶C正好在同一视线上，（点F，B，D也在同一直线上）．这一组其他同学量得标杆到树的水平距离BD=3.6m，小明到标杆的水平距离FB=2m，小明的目高（眼睛到脚底的距离）EF=1.5m．根据这些数据，小明这一组同学很快就求出了树CD的高度．你会吗？请写出解答过程．分析：过E点作EG⊥CD于G，交AB于点H，根据EF∥AB∥CD可求出EF、HB、GD，再根据相似三角形的判定定理可得△EAH∽△ECG，再根据三角形的相似比解答即可．
解答：
解：过E点作EG⊥CD于G，交AB于点H，（1分）
∵EF∥AB∥CD，
∴EF=HB=GD=1.5，
∴AH=1，（2分）
∵AH∥CG，
∴△EAH∽△ECG，（2分）
∴EH：EG=AH：CG，
2：5.6=1：CG，
∴CG=2.8，（4分）
∴CD=2.8+1.5=4.3m．（1分）
答：树CD的高度为4.3m．
解：过E点作EG⊥CD于G，交AB于点H，（1分）∵EF∥AB∥CD，
∴EF=HB=GD=1.5，
∴AH=1，（2分）
∵AH∥CG，
∴△EAH∽△ECG，（2分）
∴EH：EG=AH：CG，
2：5.6=1：CG，
∴CG=2.8，（4分）
∴CD=2.8+1.5=4.3m．（1分）
答：树CD的高度为4.3m．
点评：此题难度不大，解答此题的关键是作出辅助线．构造出相似三角形，利用平行线的性质及相似三角形的相似比解答．
练习册系列答案
相关题目
