题目内容
在Rt△ABC中,AB=6,BC=10,∠A=90°,求AC的长.
考点:勾股定理
专题:
分析:根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC2=AC2+AB2,结合BC=10,AB=6,可求出另一条直角边AC的长度.
解答:解:在直角△ABC中,
∵∠A=90°,
∴BC为斜边,
则BC2=AC2+AB2,
又∵AB=6,BC=10,
∴AC=
=8.
∵∠A=90°,
∴BC为斜边,
则BC2=AC2+AB2,
又∵AB=6,BC=10,
∴AC=
| BC2-AB2 |
点评:本题考查了勾股定理的知识,属于基础题目,像这类直接考查定义的题目,解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列语句是命题的是( )
| A、相等的角是对顶角 |
| B、同位角相等吗? |
| C、国庆60周年大阅兵好壮观呀! |
| D、过一点作已知直线的垂线 |
 如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.
如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.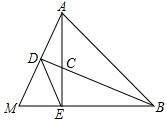 如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.
如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.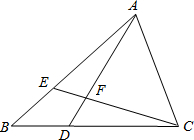 如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.
如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.