题目内容
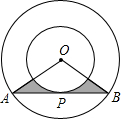
 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是
- A.9
 -π
-π - B.6
 -π
-π - C.9
 -3π
-3π - D.6
 -2π
-2π
C
分析:根据图形可明显地看出阴影部分的面积为△OAB和扇形OCD的面积差.连接OP,可根据两圆的半径长求出AP的长和扇形OCD的圆心角.然后分别计算出△OAB和扇形OCD的面积,即可求出阴影部分的面积.
解答: 解:连接OP,则OP⊥AB;
解:连接OP,则OP⊥AB;
在Rt△OBP中,BP=3 ,∠BOP=60°,
,∠BOP=60°,
∴AB=6 ,∠AOB=120°;
,∠AOB=120°;
∴S△OAB=6 ×3÷2=9
×3÷2=9 ,S扇形OCD=
,S扇形OCD= =3π,
=3π,
所以S阴影=9 -3π.
-3π.
故选C.
点评:本题的关键是理解阴影部分的面积=三角形的面积-扇形的面积,然后分别计算求值即可.
分析:根据图形可明显地看出阴影部分的面积为△OAB和扇形OCD的面积差.连接OP,可根据两圆的半径长求出AP的长和扇形OCD的圆心角.然后分别计算出△OAB和扇形OCD的面积,即可求出阴影部分的面积.
解答:
 解:连接OP,则OP⊥AB;
解:连接OP,则OP⊥AB;在Rt△OBP中,BP=3
 ,∠BOP=60°,
,∠BOP=60°,∴AB=6
 ,∠AOB=120°;
,∠AOB=120°;∴S△OAB=6
 ×3÷2=9
×3÷2=9 ,S扇形OCD=
,S扇形OCD= =3π,
=3π,所以S阴影=9
 -3π.
-3π.故选C.
点评:本题的关键是理解阴影部分的面积=三角形的面积-扇形的面积,然后分别计算求值即可.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )A、9
| ||
B、6
| ||
C、9
| ||
D、6
|
 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB= 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB= 如图,两同心圆的圆心为O,大圆的弦AB、AC分别切小圆于D、E两点,小圆的劣弧
如图,两同心圆的圆心为O,大圆的弦AB、AC分别切小圆于D、E两点,小圆的劣弧