Question

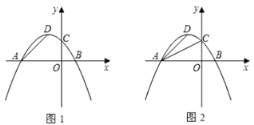
【题目】 如图1，在Rt△ABC中，∠ACB=90°，E是边AC上任意一点（点E与点A，C不重合），以CE为一直角边作Rt△ECD，∠ECD=90°，连接BE，AD．

（1）若CA=CB，CE=CD

①猜想线段BE，AD之间的数量关系及所在直线的位置关系，直接写出结论；

②现将图1中的Rt△ECD绕着点C顺时针旋转锐角α，得到图2，请判断①中的结论是否仍然成立，若成立，请证明；若不成立，请说明理由；

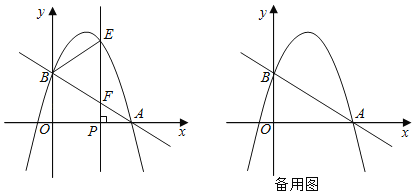
（2）若CA=8,CB=6，CE=3，CD=4，Rt△ECD绕着点C顺时针转锐角α，如图3，连接BD，AE，计算的值．

Answer 1

【答案】（1）①BE=AD，BE⊥AD；②见解析；（2）125．

【解析】

试题根据三角形全等的判定与性质得出BE=AD，BE⊥AD；设BE与AC的交点为点F，BE与AD的交点为点G，根据∠ACB=∠ECD=90°得出∠ACD=∠BCE，然后结合AC=BC，CD=CE得出△ACD≌△BCE，则AD=BE，∠CAD=∠CBF，根据∠BFC=∠AFG，∠BFC+∠CBE=90°得出∠AFG+∠CAD=90°，从而说明垂直；首先根据题意得出△ACD∽△BCE，然后说明∠AGE=∠BGD=90°，最后根据直角三角形的勾股定理将所求的线段转化成已知的线段得出答案．

试题解析：（1）①解：BE=AD，BE⊥AD

②BE=AD，BE⊥AD仍然成立

证明：设BE与AC的交点为点F，BE与AD的交点为点G，如图1．

∵∠ACB=∠ECD=90°， ∴∠ACD=∠BCE ∵AC=BC CD=CE ∴△ACD≌△BCE

∴AD=BE ∠CAD=∠CBF ∵∠BFC=∠AFG ∠BFC+∠CBE=90° ∴∠AFG+∠CAD=90°

∴∠AGF=90° ∴BE⊥AD

（2）证明：设BE与AC的交点为点F，BE的延长线与AD的交点为点G，如图2．

∵∠ACB=∠ECD=90°， ∴∠ACD=∠BCE ∵AC=8，BC=6，CE=3，CD=4 ∴△ACD∽△BCE

∴∠CAD=∠CBE ∵∠BFC=∠AFG ∠BFC+∠CBE=90° ∴∠AFG+∠CAD=90°

∴∠AGF=90° ∴BE⊥AD ∴∠AGE=∠BGD=90°

∴，．∴．

∵，，

∴