题目内容
7.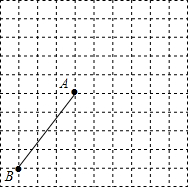 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.(1)在方格纸中将线段AB绕A点旋转,得到线段AC,点C落在校正方形的顶点上,连接BC,且△ABC的面积为10;
(2)在方格纸中画,以AC所在直线为对称轴,作△ACB的轴对称图形△ACD,连接BD.直接写出∠BDC的正弦值.
分析 (1)由于AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,而△ABC的面积为10,则点B到AC的距离为4,然后再过点A的水平格线上取5个单位即可得到C点,从而得到△ABC;
(2)作点B关于直线AC的对称点D,则可得到△ADC,BD与直线AC相交于点E,计算出DC和CE,然后利用正弦的定义可计算出∠BDC的正弦值.
解答 解:(1)如图,△ABC为所作;
(2)如图,△ACD为所求作,tan∠BDC=$\frac{8}{4\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.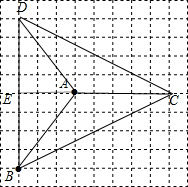
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
相关题目
16.已知m是方程x2-2x-1=0的一个根,则代数式m2-2m的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.若a=b,则下列各式不一定成立的是( )
| A. | a-1=b-1 | B. | $\frac{a}{2}$=$\frac{b}{2}$ | C. | -a=-b | D. | $\frac{a}{c}$=$\frac{b}{c}$ |