题目内容
17.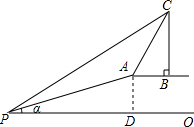 如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且tanα=$\frac{7}{24}$,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达坡顶A处,在A处测得塔顶C的仰角为60°.
如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且tanα=$\frac{7}{24}$,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达坡顶A处,在A处测得塔顶C的仰角为60°.(1)求斜坡的高度AD;
(2)求塔高BC.
分析 (1)在Rt△APD中,根据tanα的值设AD=7k,PD=24k,利用勾股定理表示出AP,根据AP=50,求出k的值,继而可求得AD的长度;
(2)延长CB交PO于点E,设塔高为x,在Rt△CBA中,求出AB的长度,然后在Rt△PCE中,根据∠CPE=30°,利用三角函数求解.
解答 解:(1)在Rt△APD中,
∵tanα=$\frac{7}{24}$,
∴设AD=7k,PD=24k,
∴PA=$\sqrt{(7k)^{2}+(24k)^{2}}$=25k,
∵PA=50,
∴AD=APsinα=50×$\frac{7}{25}$=14(m);
(2)延长CB交PO于点E,可得四边形ABED为矩形,
设塔高为x,
在Rt△CBA中,
∵∠CAB=60°,tan60°=$\frac{BC}{AB}$,
∴AB=$\frac{x}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$x,
在Rt△CPE中,
∵∠CPE=30°,
∴$\frac{CE}{PE}$=tan30°,
即$\frac{x+14}{48+\frac{\sqrt{3}}{3}x}$=$\frac{\sqrt{3}}{3}$,
解得:x=24$\sqrt{3}$-21,
答:塔的高度为(24$\sqrt{3}$-21)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡度和仰角构造直角三角形,利用三角函数的知识解直角三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
12. 如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
 如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
6.比较π,-1,3的大小,下列判断正确的是( )
| A. | π<-1<3 | B. | -1<π<3 | C. | -1<3<π | D. | 3<-1<π |
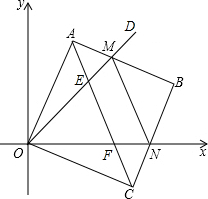 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在第一象限的角平分线OD上时停止旋转,旋转过程中,AB边交OD于点M,BC边交x轴于点N,AC与OD相交于点E,与x轴相交于点F.(如图).
在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在第一象限的角平分线OD上时停止旋转,旋转过程中,AB边交OD于点M,BC边交x轴于点N,AC与OD相交于点E,与x轴相交于点F.(如图).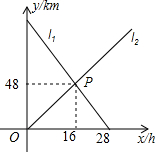 如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.
如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.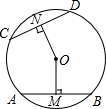 如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB=CD,求证:OM=ON.
如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB=CD,求证:OM=ON.