题目内容
18.一个不透明袋中有红、黄、绿三种颜色的球共36个,它们除颜色外都相同,其中黄球个数是绿球个数的2倍.已知从袋中摸出一个球是红球的概率为$\frac{1}{3}$.(1)求绿球的个数;
(2)若从袋中拿出4个黄球,求从袋中随机摸出一个球是黄球的概率.
分析 (1)先求出红球的个数,设绿球的个数为x个,根据黄球个数是绿球个数的2倍,列出方程求解即可;
(2)先求出黄球的个数,再根据概率公式计算即可.
解答 解:(1)∵从袋中摸出一个球是红球的概率为$\frac{1}{3}$,
∴红球的个数是:36×$\frac{1}{3}$=12(个),
设绿球的个数为x个,根据题意得:
x+2x=36-12=24,
解得:x=8,
答:绿球的个数是8个;
(2)根据题意得:黄球的个数是:2×8-4=12(个),
则从袋中随机摸出一个球是黄球的概率为:$\frac{12}{36-4}$=$\frac{3}{8}$.
点评 本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
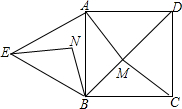 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.