Question

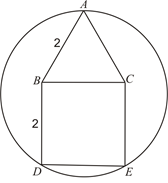
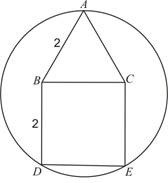
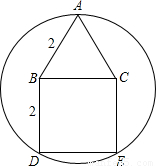
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成，一圆过A、D、E三点，求该圆半径的长．

 

Answer 1

【答案】

2

【解析】

试题分析：解：如图，

将正方形BDEC上的等边△ABC向下平移得等边△ODE，其底边与DE重合，

∵A、B、C的对应点是O、D、E，

∴OD=AB，OE=AC，AO=BD，

∵等边△ABC和正方形BDEC的边长都是2，

∴AB=BD=AC=2，

∴OD =OA=OE=2，

∵A、D、E三点不在同一直线上，

∴A、D、E三点确定一圆，

∵O到A、D、E三点的距离相等，

∴O点为圆心，OA为半径，

∴该圆的半径长为2。

考点：圆

点评：本题难度较大，主要考查学生对圆和其他几何图形综合运用能力。为中考常见题型，学生要牢固掌握各几何性质定理，并运用到考试中去。