Question

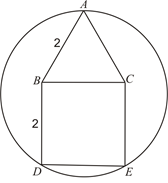
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成，一圆过A、D、E三点，求该圆半径的长．

 

Answer 1

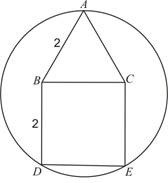
【答案】

2

【解析】解:方法一．如图1，

将正方形BDEC上的等边△ABC向下平移得等边△ODE，其底边与DE重合．………………………1分

∵A、B、C的对应点是O、D、E．

∴OD=AB，OE=AC，AO=BD．    …………………3分

∵等边△ABC和正方形BDEC的边长都是2，

∴AB=BD=AC=2．

∴OD =OA=OE=2．          ………………………4分

∵A、D、E三点不在同一直线上，

∴A、D、E三点确定一圆，  ………………………6分

∵O到A、D、E三点的距离相等，

∴O点为圆心，OA为半径．

∴该圆的半径长为2．       ………………………8分

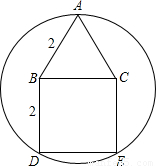
方法二．如图2，

作AF⊥BC，垂足为F，并延长交DE于H点．                      ………………1分

∵△ABC为等边三角形，

∴AF垂直平分BC，

∵四边形BDEC为正方形，

∴AH垂直平分正方形的边DE．……………………3分

又DE是圆的弦，∴AH必过圆心，记圆心为O点，并设⊙O的半径为r．

在Rt△ABF中， ∵∠BAF=，

∴．

∴OH==ｒ． ……………………………………………………5分

在Rt△ODH中， ．

∴．解得ｒ＝2．．……………………………………………………7分

∴该圆的半径长为2．                                   ………………………8分

方法不唯一，方法一：利用平移的方法，根据等边三角形的三边相等，正方形四边相等，得出A、D、E三点确定一圆即可；方法二：作垂直，利用三线合一，勾股定理，构造关于半径的方程即可