题目内容
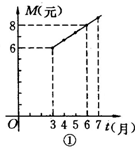
如图26-3-13①所示，某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的销售和成本进行了调研，结果如下：每件商品的售价M元与时间（月）的关系可以用一条线段上的点来表示，每件商品的成本Q（元）与时间t（月）的关系可用一条抛物线的一部分上的点来表示（如图26-3-13②所示）．
（说明：图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本）．
请你根据图象提供的信息回答：
（1）每件商品3月份出售时的利润（利润=售价-成本）是多少元？
（2）求图26-3-13②中表示的每件商品的成本Q（元）与时间t（月）之间的函数关系式（不要求写自变量的取值范围）；
（3）你能求出三月份至七月份每件商品的利润W（元）与时间t（月）之间的函数关系式吗？（请写出计算过程，不要求写自变量的取值范围），若该公司共有此种商品30000件，准备一个月内全部售完，请你计算一下至少获利多少元？
（1）5元；（2）Q=-
t2+4t-8；
（3）W=（t-5）2+
．
t=5时，W最小=元．
∴30 000件商品一个月内售完至少获得110 000元利润．
练习册系列答案
相关题目
（2013•鼓楼区一模）甲、乙两篮球运动员上赛季每场比赛的得分如下．
在2006年青岛崂山北宅樱桃节前夕，某果品批发公司为指导今年的樱桃销售，对往年的市场销售情况进行了调查统计，得到如下数据：
|
销售价 x（元/千克） |
… |
25 |
24 |
23 |
22 |
… |
|
销售量 y（千克） |
… |
2 000 |
2 500 |
3 000 |
3 500 |
… |
（1）在如图26-3-1-2的直角坐标系内，作出各组有序数对（x，y）所对应的点．连结各点并观察所得的图形，判断y与x之间的函数关系，并求出y与x之间的函数关系式；
（2）若樱桃进价为13元/千克，试求销售利润P（元）与销售价x (元/千克)之间的函数关系式，并求出当x取何值时，P的值最大？
