题目内容
如图，梯形ABCD中，AD∥BC，AC与BD相交于点O，已知
，那么S△AOB：S△BOC=________．
1：2
分析：根据三角形相似的判定方法由AD∥BC得到△AOD∽△COB，再根据相似三角形的性质得
=（
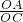）2=
，则可计算出OA：OC=1：2，然后根据三角形面积公式得到S△AOB：S△BOC=AO：OC=1：2．
解答：∵AD∥BC，
∴△AOD∽△COB，
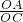∴=（）2=，
∴OA：OC=1：2，
∵S△AOB：S△BOC=AO：OC，
∴S△AOB：S△BOC=1：2．
故答案为1：2．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截得的三角形与原三角形相似；相似三角形面积的比等于相似比的平方．也考查了三角形面积公式．
分析：根据三角形相似的判定方法由AD∥BC得到△AOD∽△COB，再根据相似三角形的性质得
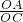=（）2=，则可计算出OA：OC=1：2，然后根据三角形面积公式得到S△AOB：S△BOC=AO：OC=1：2．解答：∵AD∥BC，
∴△AOD∽△COB，
∴
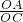=（）2=，∴OA：OC=1：2，
∵S△AOB：S△BOC=AO：OC，
∴S△AOB：S△BOC=1：2．
故答案为1：2．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截得的三角形与原三角形相似；相似三角形面积的比等于相似比的平方．也考查了三角形面积公式．
练习册系列答案
相关题目
已知，如图，梯形ABCD中，AD∥BC，∠B=45°，∠C=120°，AB=8，则CD的长为（ ）A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
5、已知：如图，梯形ABCD中，AD∥BC，AB=DC，AC、BD相交于点O，那么，图中全等三角形共有
10、如图，梯形ABCD中，AD∥BC，BD为对角线，中位线EF交BD于O点，若FO-EO=3，则BC-AD等于（ ）
如图，梯形ABCD中，已知AD∥BC，∠A=90°，AB=7，AD=2，
如图，梯形ABCD中，AD∥BC，BC=5，AD=3，对角线AC⊥BD，且∠DBC=30°，求梯形ABCD的高．